photosdematures.com

Què és Dietz modificat?

Dietz modificat fa referència a la mesura que s’utilitza per determinar el rendiment històric de la cartera dividint el flux de caixa real net de la sortida amb capital mitjà, que utilitza el pes i el valor de la cartera al principi. En un mètode Dietz simple, se suposa que tots els fluxos d'efectiu provenen de la meitat del període, mentre que no és el cas del mètode Dietz modificat.

Fórmula

La taxa de retorn de Dietz modificada es pot definir mitjançant la fórmula següent i s’explica cadascun dels termes que conté:

• ROR (Taxa de rendiment): aquest és el terme que volem calcular
• EMV (Valor de mercat final): aquest és el valor de la cartera després de finalitzar el termini que busquem.
• BMV (Valor de mercat inicial): és el valor de la cartera a partir de la data en què es calcularan els rendiments
• W (Pes de cada flux de caixa a la cartera): és el pes de la cartera entre zero i un, però només entre el període en què es van produir i al final del període. Això es pot explicar com la proporció de temps entre el moment en què es produeix el flux i el final del període. Es pot calcular mitjançant la fórmula
• W = [C- D] / C on D és el nombre de dies des de l'inici del període de retorn fins al dia en què es va produir el flux.
• C - Fluxos d'efectiu durant el període: pot ser que no sigui un nombre únic, sinó una sèrie de fluxos d'efectiu ocorreguts durant el període.
• W * C = la suma de cada flux de caixa multiplicat pel seu pes. Es tracta d’un resum dels fluxos d’efectiu ponderats

Exemples

A continuació es mostren alguns exemples del mètode Dietz modificat.

Exemple 1

Considerem un escenari molt senzill amb les següents condicions:

• Tenim una cartera d’1 milió de dòlars americans al començament del període d’inversió.
• Després de dos anys, el valor de la cartera ha crescut fins als 2,3 milions de dòlars.
• Hi va haver una entrada de 0,5 milions de dòlars americans al cap d’un any.

Ara, calcularem com s’utilitzarà el mètode Dietz modificat per calcular els rendiments d’aquesta cartera.

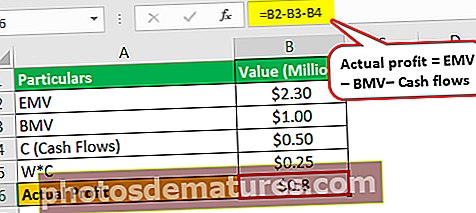
• Benefici real = EMV (2,3 milions de dòlars) - BMV (1 milió de dòlars) - Fluxos de caixa (0,5 milions de dòlars d’entrada)
• =$0.8

Això comporta un benefici de 0,8 milions de dòlars.

Ara vegem quin era el capital mitjà en aquest cas.

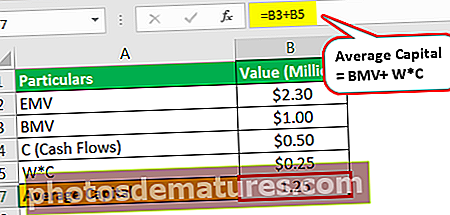
• Capital mitjà = BMV (1 milió de dòlars) + W * C (0,5 milions de dòlars * 0,5 Període de temps)
• = 1.25

Per tant, la taxa de rendiment serà:

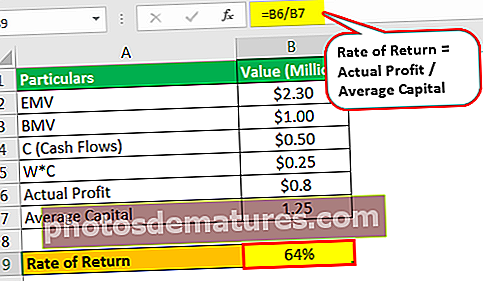
• Taxa de rendiment = benefici real / capital mitjà
• = $0.8 / 1.25
• = 64%

Exemple 2

Comparació de Dietz modificada amb la taxa de retorn ponderada en el temps

Considerem dos inversors amb les següents carteres.

1. L'inversor A va començar amb una cartera de 250.000 USD al començament d’un any (gener) i va utilitzar les seves estratègies per fer-ho 298.000 USD a finals del mateix any (desembre). No obstant això, va posar un capital addicional de 25.000 dòlars americans durant el setembre.
2. L'inversor B va començar amb una cartera de 250.000 USD a principis d'any (gener), i va utilitzar les seves estratègies, però va acabar amb 251.000 USD a finals d'any. No obstant això, va retirar 25.000 milions durant el setembre.

A simple vista, o utilitzant les matemàtiques elementals a la nostra ment, podem dir que l’inversor B és invertit malament que l’inversor A. No obstant això, aprofundir en els càlculs ens donarà completament una altra cara de la història.

Per a l’inversor A:

El benefici real serà -

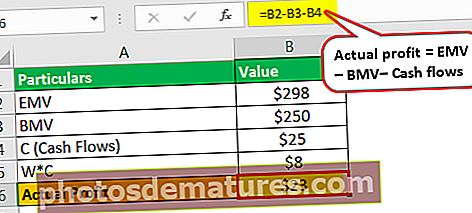
• Benefici real = (298.000 USD - 250.000 USD - 25.000 USD)
• = 23.000 USD

El període mitjà serà de -

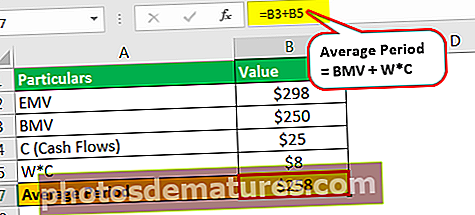
• Període mitjà = 250.000 USD + (25.000 USD * 0.3)
• = 258.000 USD

La taxa de Dietz modificada serà -

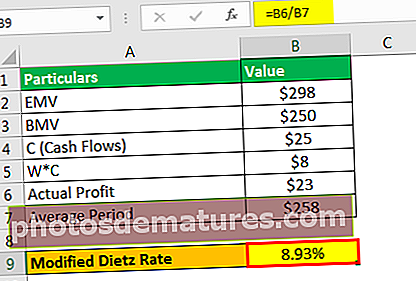
• Taxa de Dietz modificada = 8,7%

Per a l’inversor B:

El benefici real serà -

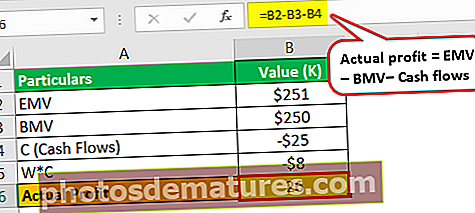
• Benefici real = (251.000 USD - 250.000 USD + 25.000 USD)
• = 26.000 USD

El període mitjà serà de -

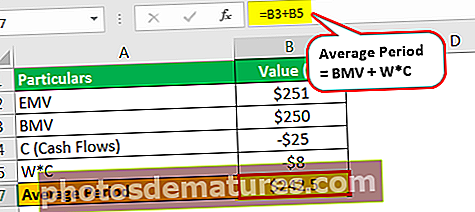
• Període mitjà = 250.000 USD + (-25.000 USD * 0.3)
• = 242,5 k USD

La taxa de Dietz modificada serà -

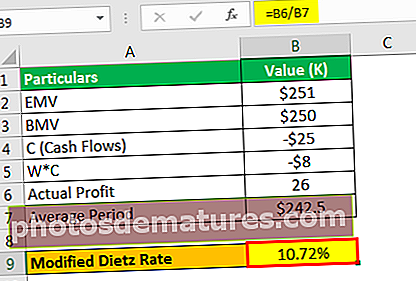
• Taxa de Dietz modificada = 10,72%

La taxa de retorn ponderada en el temps per als dos anteriors rondarà el 9,5, però Dietz modificat ens va donar resultats diferents. Aquesta és la raó per la qual aquest mètode és utilitzat pels inversors per informar.

Avantatges

• El principal avantatge d’aquest mètode és que no requereix valoració de cartera en cada data del flux de caixa. Això ajuda l'analista a afirmar el valor dels rendiments fàcilment, sense tornar a avaluar-ho cada vegada.
• Hi ha atribucions de rendiment que no estan disponibles amb altres mètodes de ponderació del temps; durant aquests casos, el mètode Dietz modificat és útil.
• Casos com l'exemple 2 en què la taxa de rendibilitat ponderada en el temps no és una mesura adequada.

Limitacions

• Amb l’avanç en informàtica, la majoria de les rendibilitats actuals es calculen de forma contínua; proporcionen una manera millor d’analitzar els mètodes de devolució i de sortida, com ara Dietz modificat, de manera molt ingènua i bàsica.
• Un supòsit de que totes les transaccions es produeixin simultàniament en un sol punt en un període de temps comportarà errors
• És molt difícil fer front a fluxos de caixa negatius o de mitjana zero.

Conclusió

A mesura que la normativa al voltant del sector financer creix, els inversors han de tenir més cura en quant es calculen la inversió i els rendiments i com s’informa. Aquest mètode de Dietz modificat proporciona una confiança raonable en l'anàlisi dels rendiments de la inversió.

El mètode Dietz modificat només ens proporciona una mesura dels rendiments de les carteres d’inversió on hi ha múltiples entrades i sortides. Actualment, amb una informàtica avançada i una gestió contínua de devolucions, aquest mètode no és útil. Tot i això, el concepte bàsic darrere del mètode és útil per entendre com funcionen els rendiments i els seus càlculs.