Fórmula de la variant de la població | Càlcul pas a pas | Exemples
Fórmula per calcular la variació de la població
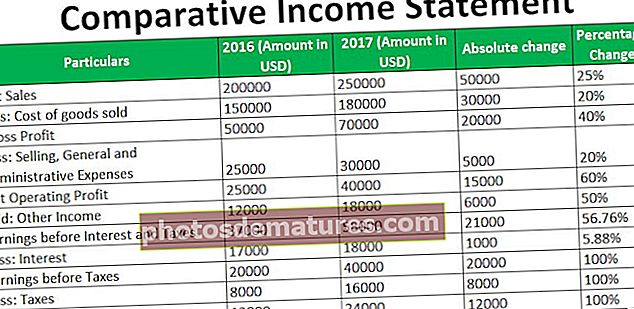
La fórmula de la variància de la població es mesura per les distàncies mitjanes de les dades de la població i es calcula esbrinant la mitjana de la fórmula de la població i la variància es calcula per la suma del quadrat de variables menys la mitjana que es divideix per un nombre d’observacions a la població.
La variància de la població és una mesura de la difusió de les dades de població. Per tant, la variància de la població es pot definir com la mitjana de les distàncies des de cada punt de dades d’una població concreta fins a la mitjana, al quadrat i indica com es distribueixen els punts de dades a la població. La variància de la població és una mesura important de la dispersió que s’utilitza a les estadístiques. Els estadístics calculen la variància per determinar com es relacionen els números individuals d’un conjunt de dades.
Mentre es calcula la variància de la població, la dispersió es calcula en referència a la mitjana de la població. Per tant, hem d’esbrinar la mitjana de la població per calcular la variància de la població. Una de les notificacions més populars de la variància poblacional és σ2. Això es pronuncia com a sigma al quadrat.
La variància de la població es pot calcular mitjançant la fórmula següent:


on
- σ2 és la variància de la població,
- x1, x2, x3,... ..xn són les observacions
- N és el nombre d'observacions,
- µ és la mitjana del conjunt de dades
Càlcul pas a pas de la variació de la població
La fórmula per a la variància poblacional es pot calcular mitjançant els cinc passos simples següents:
- Pas 1: Calculeu la mitjana (µ) de les dades donades. Per calcular la mitjana, afegiu totes les observacions i després dividiu-la pel nombre d'observacions (N).
- Pas 2: Feu una taula. Tingueu en compte que la construcció d’una taula no és obligatòria, però presentar-la en format tabular facilitaria els càlculs. A la primera columna, escriviu cada observació (x1, x2, x3,... ..xn).
- Pas 3: A la segona columna, escriviu la desviació de cada observació de la mitjana (xjo - µ).
- Pas 4: A la tercera columna, escriviu el quadrat de cada observació a partir de la mitjana (xjo - µ) 2. Dit d’una altra manera, quadra cadascun dels números obtinguts a la columna 2.
- Pas 5: Posteriorment, hem d'afegir els números obtinguts a la tercera columna. Trobeu la suma de les desviacions quadrades i dividiu la suma obtinguda pel nombre d'observacions (N). Això ens ajudarà a obtenir
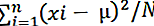 que és la variància poblacional.
que és la variància poblacional.
Exemples
Podeu descarregar aquesta plantilla Excel de fórmula de variació de població aquí: plantilla Excel de fórmula de variació de poblacióExemple 1
Calculeu la variància poblacional a partir de les 5 observacions següents: 50, 55, 45, 60, 40.
Solució:
Utilitzeu les dades següents per al càlcul de la variància poblacional.

Hi ha un total de 5 observacions. Per tant, N = 5.
µ = (50 + 55 + 45 + 60 + 40) / 5 = 250/5 = 50
Per tant, el càlcul de la variància de la població σ2 es pot fer de la següent manera:


σ2 = 250/5
La variació de la població σ2 serà-

Variació de la població (σ2) = 50
La variància poblacional és de 50.
Exemple 2
XYZ Ltd. és una empresa petita i consta de només 6 empleats. El conseller delegat creu que no hauria d’haver una dispersió elevada en els salaris d’aquests empleats. Amb aquest propòsit, vol que calculeu la variància d'aquests salaris. Els sous d’aquests empleats són iguals. Calculeu la variància poblacional dels sous del conseller delegat.
Solució:
Utilitzeu les dades següents per al càlcul de la variància poblacional.

Hi ha un total de 6 observacions. Per tant, N = 6.
=(30+27+20+40+32+31)/6 =180/6 =$ 30
Per tant, el càlcul de la variància poblacional σ2 es pot fer de la següent manera:


σ2 = 214/6
La variació de la població σ2 serà-

Variació de la població (σ2) = 35,67
La variació poblacional dels salaris és de 35,67.
Exemple 3
Sweet Juice Ltd fabrica diferents sabors de suc. El Departament de Gestió compra 7 grans contenidors per emmagatzemar aquest suc a la fàbrica. El Departament de Control de Qualitat ha decidit que rebutjarà els contenidors si la variància dels envasos és superior a 10. Es donen els pesos de 7 contenidors en kg: 105, 100, 102, 95, 100, 98 i 107. Informeu la Qualitat Departament de control sobre si ha de rebutjar els contenidors.
Solució:
Utilitzeu les dades següents per al càlcul de la variància poblacional.

Hi ha un total de 7 observacions. Per tant, N = 7
=(105+100+102+95+100+98+107)/7 =707/7 =10
Per tant, el càlcul de la variància de la població σ2 es pot fer de la següent manera:


σ2 = 100/7
La variació de la població σ2 serà

Variació de la població (σ2) = 14,29
Atès que la variància (14.29) supera el límit de 10 decidit pel departament de control de qualitat, els contenidors haurien de ser rebutjats.
Exemple # 4
L’equip directiu d’un hospital anomenat Sagar Healthcare va registrar que havien nascut 8 nadons la primera setmana de març del 2019. El metge volia avaluar la salut dels nadons i la variància de les altures. Les alçades d’aquests nadons són les següents: 48 cm, 47 cm, 50 cm, 53 cm, 50 cm, 52 cm, 51 cm, 60 cm. Calculeu la variància de les altures d’aquests vuit nadons.
Solució:
Utilitzeu les dades següents per al càlcul de la variància poblacional.

Per tant, el càlcul de la variància poblacional σ2 es pot fer de la següent manera:

A Excel, hi ha una fórmula incorporada per a la variància de la població que es pot utilitzar per calcular la variància de la població d’un grup de nombres. Seleccioneu una cel·la en blanc i escriviu aquesta fórmula = VAR.P (B2: B9). Aquí, B2: B9 és l’interval de cel·les des del qual voleu calcular la variància de la població.
La variació de la població σ2 serà

Variació de la població (σ2) = 13.98
Rellevància i ús
La variació de la població s’utilitza com a mesura de dispersió. Considerem dos conjunts de població amb la mateixa mitjana i nombre d’observacions. El conjunt de dades 1 consta de 5 nombres: 55, 50, 45, 50 i 50. El conjunt de dades 2 consta de 10, 50, 85, 90 i 15. Tots dos conjunts de dades tenen la mateixa mitjana, que és 50. Però, al conjunt de dades 1, els valors són propers entre si, mentre que el conjunt de dades 2 té valors dispersos. La variància dóna una mesura científica d'aquesta proximitat / dispersió. El conjunt de dades 1 només té una variància de 10, mentre que el conjunt de dades 2 té una enorme variant de 1130. Per tant, una gran variància indica que les xifres estan lluny de la mitjana i les unes de les altres. Una petita variància indica que les xifres són properes entre si.
La variació s’utilitza en el camp de la gestió de carteres mentre es realitza l’assignació d’actius. Els inversors calculen la variància de la rendibilitat dels actius per determinar les carteres òptimes optimitzant els dos paràmetres principals: la rendibilitat i la volatilitat. La volatilitat mesurada per variància és una mesura del risc d’una seguretat financera concreta.

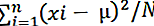 que és la variància poblacional.
que és la variància poblacional.