photosdematures.com

Què és R Squared (R2) en regressió?

El quadrat R (R2) és una mesura estadística important que és un model de regressió que representa la proporció de la diferència o de la variància en termes estadístics per a una variable dependent que es pot explicar per una variable o variables independents. En resum, determina el grau d’adequació de les dades al model de regressió.

R Fórmula quadrada

Per al càlcul de R al quadrat, heu de determinar el coeficient de correlació i després heu de quadrar el resultat.

R Fórmula quadrada = r2

On r es pot calcular el coeficient de correlació a continuació:

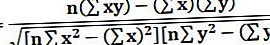
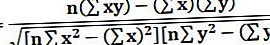
On,

• r = El coeficient de correlació
• n = número del conjunt de dades donat
• x = primera variable del context
• y = segona variable

Explicació

Si hi ha alguna relació o correlació que pugui ser lineal o no lineal entre aquestes dues variables, indicarà si hi ha un canvi en el valor de la variable independent, llavors l’altra variable dependent probablement canviarà de valor, per exemple, linealment o no linealment.

La part numeradora de la fórmula realitza una prova de si es mouen junts i elimina els seus moviments individuals i la força relativa de tots dos movent-se junts i la part denominadora de la fórmula escala el numerador prenent l’arrel quadrada del producte de les diferències de la variables de les seves variables quadrades. I quan es quadra aquest resultat, obtenim un quadrat R que no és res més que el coeficient de determinació.

Exemples

Podeu descarregar aquesta plantilla R Squared Formula Excel aquí: plantilla R Squared Formula Excel

Exemple 1

Considereu les dues variables següents x i y, heu de calcular el R quadrat en regressió.

Solució:

Utilitzant la fórmula esmentada, primer hem de calcular el coeficient de correlació.

Tenim tots els valors de la taula anterior amb n = 4.

Introduïu ara els valors de la fórmula per arribar a la figura.

r = (4 * 26.046,25) - (265,18 * 326,89) / √ [(4 * 21,274,94) - (326,89) 2] * [(4 * 31,901,89) - (326,89) 2]

r = 17.501,06 / 17.512,88

El coeficient de correlació serà

r = 0,99932480

Per tant, el càlcul serà el següent,

r2 = (0,99932480) 2

R Fórmula quadrada en regressió

r2 = 0,998650052

Exemple 2

L'Índia, un país en desenvolupament, vol fer una anàlisi independent si els canvis en els preus del cru han afectat el seu valor en rupies. A continuació es mostra la història del preu del cru de Brent i de la valoració de la rupia ambdós contra dòlars que prevalien de mitjana per aquells anys per sota.

RBI, el banc central de l'Índia, s'ha acostat a vosaltres per fer una presentació sobre el mateix en la propera reunió. Determineu si els moviments del cru afecten els moviments en rupia per dòlar?

Solució:

Utilitzant la fórmula de la correlació anterior, podem calcular primer el coeficient de correlació. Tractant el preu mitjà del cru com una variable, per exemple, x i tractant la rupia per dòlar com una altra variable com y.

Tenim tots els valors de la taula anterior amb n = 6.

Introduïu ara els valors de la fórmula per arribar a la figura.

r = (6 * 23592,83) - (356,70 * 398,59) / √ [(6 * 22829,36) - (356,70) 2] * [(6 * 26529,38) - (398,59) 2]

r = -620,06 / 1.715,95

El coeficient de correlació serà

r = -0,3614

Per tant, el càlcul serà el següent,

r2 = (-0,3614) 2

R Fórmula quadrada en regressió

r2 = 0.1306

Anàlisi: Sembla que hi ha una relació menor entre els canvis en els preus del cru i els canvis en el preu de la rupia índia. A mesura que augmenta el preu del cru, els canvis en la rupia índia també afecten. Però, atès que el R quadrat és només del 13%, els canvis en el preu del cru expliquen molt menys els canvis de la rupia índia i la rupia índia també està subjecta a canvis en altres variables que cal tenir en compte.

Exemple 3

El laboratori XYZ està realitzant investigacions sobre alçada i pes i està interessat en saber si hi ha algun tipus de relació entre aquestes variables. Després de reunir una mostra de 5.000 persones per a cada categoria i es va trobar amb un pes mitjà i una alçada mitjana en aquest grup en concret.

A continuació es detallen els detalls que han reunit.

Heu de calcular R al quadrat i concloure si aquest model explica que les variàncies d’altura afecten les variacions de pes.

Solució:

Utilitzant la fórmula de la correlació anterior, podem calcular primer el coeficient de correlació. Tractant l'alçada com una variable, digueu x i tractant el pes com una altra variable com a y.

Tenim tots els valors de la taula anterior amb n = 6.

Introduïu ara els valors de la fórmula per arribar a la figura.

r = (7 * 74,058,67) - (1031 * 496,44) / √ [(7 * 153595 - (1031) 2] * [(7 * 35793,59) - (496,44) 2]

r = 6.581,05 / 7.075,77

El coeficient de correlació serà

Coeficient de correlació (r) = 0,930

Per tant, el càlcul serà el següent,

r2 = 0,865

Anàlisi: La correlació és positiva i sembla que hi ha alguna relació entre l'alçada i el pes, ja que l'alçada augmenta; el pes de la persona també sembla augmentar-se. Tot i que R2 suggereix que el 86% dels canvis d’alçada s’atribueixen a canvis de pes i el 14% són inexplicables.

Rellevància i usos

La rellevància de R al quadrat en regressió és la seva capacitat per trobar la probabilitat que es produeixin esdeveniments futurs dins dels resultats predits o els resultats previstos. Si s'afegeixen més mostres al model, el coeficient mostrarà la probabilitat o la probabilitat que un nou punt o el nou conjunt de dades caigui sobre la línia. Fins i tot si ambdues variables tenen una forta connexió, la determinació no demostra la causalitat.

Alguns dels espais on s’utilitza majoritàriament R quadrat són per al seguiment del rendiment dels fons d'inversió, per al seguiment del risc en els fons de cobertura, per determinar el grau de moviment de les accions amb el mercat, on R2 suggeriria quina quantitat dels moviments de les accions es poden explicar pels moviments del mercat.