photosdematures.com

Quin és el coeficient de variació?

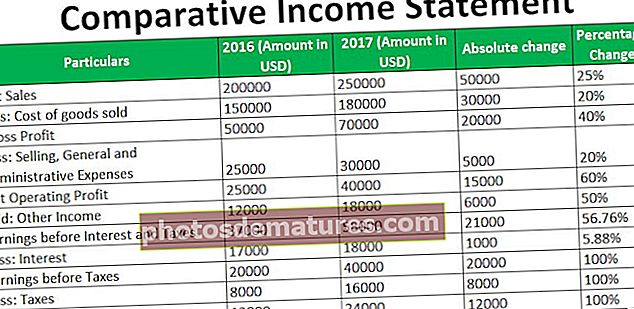
El coeficient de variació es refereix a la mesura estadística que ajuda a mesurar la dispersió dels diversos punts de dades de la sèrie de dades al voltant de la mitjana i es calcula dividint la desviació estàndard per mitja i multiplicant la resultant per 100.

Fórmula del coeficient de variació

El terme "coeficient de variació" fa referència a la mètrica estadística que s'utilitza per mesurar la variabilitat relativa en una sèrie de dades al voltant de la mitjana o per comparar la variabilitat relativa d'un conjunt de dades amb la d'altres conjunts de dades, fins i tot si la seva mètrica absoluta pot ser dràsticament diferent. Matemàticament, la fórmula del coeficient de variació es representa com,

Fórmula del coeficient de variació = Desviació estàndard / Mitjana

Es pot expressar com es mostra a continuació,

 on

• X_jo = ith variable aleatòria
• X = Mitjana de la sèrie de dades
• N = Nombre de variables de la sèrie de dades

Càlcul pas a pas

El càlcul de l'equació de coeficient de variació es pot fer seguint els passos següents:

• Pas 1: En primer lloc, esbrineu les variables aleatòries que formen part d’una gran sèrie de dades. Aquestes variables es denoten amb X_jo.
• Pas 2: A continuació, determineu el nombre de variables de la sèrie de dades que es denota amb N.
• Pas 3: A continuació, determineu la mitjana de les sèries de dades resumint inicialment totes les variables aleatòries de la sèrie de dades i dividint el resultat pel nombre de variables de la sèrie. La mitjana mostral es denota amb X.
• Pas 4: A continuació, calculeu la desviació estàndard de les sèries de dades en funció de les desviacions de cada variable de la mitjana i del nombre de variables de la sèrie de dades.
• Pas 5: Finalment, l’equació del coeficient de variació es calcula dividint la desviació estàndard de la sèrie de dades per la mitjana de la sèrie.

Exemple

Podeu descarregar aquesta plantilla Excel de fórmula de coeficient de variació aquí - Plantilla Excel de fórmula de coeficient de variació

Prenguem l'exemple del moviment del preu de les accions d'Apple Inc. del 14 de gener de 2019 al 13 de febrer de 2019. Calculeu el coeficient de variació del preu de les accions d'Apple Inc. per al període determinat.

A continuació es mostren les dades per calcular el coeficient de variació d’Apple Inc.

Càlcul de la mitjana

A partir dels preus de les accions esmentats anteriorment, podem calcular el preu mitjà de les accions del període que es pot calcular com:

Preu mitjà de les accions = Suma dels preus de les accions / Nombre de dies (sumeu tots els preus de les accions i dividiu-los pel nombre de dies; el càlcul detallat es menciona a l’última secció de l’article)

= 3569.08 / 22

Mitjana = 162,23 dòlars

Càlcul de la desviació estàndard

A continuació, determineu la desviació de cada preu de les accions respecte del preu mitjà de les accions. Es mostra a la tercera columna, mentre que el quadrat de la desviació es calcula a la quarta columna.

Ara, la desviació estàndard es calcula sobre la base de la suma de les desviacions quadrades i del nombre de dies que,

Desviació estàndard = (Suma de desviacions quadrades / Nombre de dies) 1/2

= (1454.7040 / 22)1/2

Desviació estàndard = 8,13 dòlars

Càlcul de coeficients

= $8.13 / $162.23

El coeficient serà -

Per tant, el coeficient del preu de les accions d’Apple Inc. per al període donat és de 0,0501, que també es pot expressar ja que la desviació estàndard és del 5,01% de la mitjana.

Rellevància i ús

És important entendre el concepte de fórmula de coeficient de variació perquè permet a un inversor avaluar el risc o la volatilitat en comparació amb la quantitat de rendiment esperat de la inversió. Tingueu en compte que, a mesura que baixi el coeficient, millor serà la compensació risc-retorn. No obstant això, hi ha una limitació d'aquesta relació que si el rendiment mitjà o esperat és negatiu o nul, el coeficient podria ser enganyós (ja que la mitjana és el denominador d'aquesta relació).