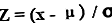photosdematures.com

Fórmula per calcular el Z-Score

La puntuació Z de les dades brutes es refereix a la puntuació generada mesurant quantes desviacions estàndard superiors o inferiors a la mitjana de la població són les dades, cosa que ajuda a provar la hipòtesi considerada. En altres paraules, és la distància d’un punt de dades de la mitjana de la població que s’expressa com a múltiple de la desviació estàndard.

• Les puntuacions z varien en el rang de -3 vegades la desviació estàndard (a l'esquerra de la distribució normal) fins a +3 vegades la desviació estàndard (a l'extrem dret de la distribució normal).
• Les puntuacions z tenen una mitjana de 0 i una desviació estàndard d'1.

L'equació per a la puntuació z d'un punt de dades es calcula restant la mitjana de la població del punt de dades (anomenat x) i el resultat es divideix per la desviació estàndard de la població. Matemàticament, es representa com,

Puntuació Z = (x - μ) / ơ

on

• x = Punt de dades
• μ = Mitjana
• ơ = Desviació estàndard

Càlcul de la puntuació Z (pas a pas)

L'equació per a la puntuació z d'un punt de dades es pot obtenir seguint els passos següents:

• Pas 1: En primer lloc, determineu la mitjana del conjunt de dades en funció dels punts de dades o observacions que es denoten amb x_jo, mentre que el nombre total de punts de dades del conjunt de dades es denota amb N.

• Pas 2: A continuació, determineu la desviació estàndard de la població en funció de la mitjana de la població μ, punts de dades x_jo i el nombre de punts de dades de la població N.

• Pas 3: Finalment, la puntuació z es deriva restant la mitjana del punt de dades i després el resultat es divideix per la desviació estàndard, tal com es mostra a continuació.

  

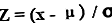
Exemples

Podeu descarregar aquesta plantilla de fórmula Excel de puntuació Z aquí: plantilla de fórmula Excel de puntuació Z

Exemple 1

Posem l'exemple d'una classe de 50 estudiants que han escrit la prova de ciències la setmana passada. Avui és el dia del resultat i el professor de la classe ha dit que John va obtenir 93 puntuacions a la prova, mentre que la puntuació mitjana de la classe va ser de 68. Determineu la puntuació z de la nota de prova de John si la desviació estàndard és de 13.

Solució:

Atès,

• Puntuació de la prova de John, x = 93
• Mitjana, μ = 68
• Desviació estàndard, ơ = 13

Per tant, la puntuació z de la puntuació de la prova de John es pot calcular utilitzant la fórmula anterior com:

Z = (93 - 68) / 13

La puntuació Z serà -

Puntuació Z = 1,92

Per tant, la puntuació de John’s Ztest és d’1,92 desviació estàndard per sobre de la puntuació mitjana de la classe, cosa que significa que el 97,26% de la classe (49 estudiants) va obtenir menys de John.

Exemple 2

Prenem un altre exemple detallat de 30 estudiants (ja que la prova z no és adequada per a menys de 30 punts de dades) que van aparèixer a una prova de classe. Determineu la puntuació de la prova z del 4t alumne en funció de les notes obtingudes pels estudiants entre 100 - 55, 67, 84, 65, 59, 68, 77, 95, 88, 78, 53, 81, 73, 66 , 65, 52, 54, 83, 86, 94, 85, 72, 62, 64, 74, 82, 58, 57, 51, 91.

Solució:

Atès,

• x = 65,
• 4t alumne puntuat = 65,
• Nombre de punts de dades, N = 30.

Mitjana = (55 + 67 + 84 + 65 + 59 + 68 + 77 + 95 + 88 + 78 + 53 + 81 + 73 + 66 + 65 + 52 + 54 + 83 + 86 + 94 + 85 + 72 + 62 + 64 + 74 + 82 + 58 + 57 + 51 + 91) / 30

Mitjana = 71,30

Ara, la desviació estàndard es pot calcular mitjançant la fórmula que es mostra a continuació,

ơ = 13,44

Per tant, la puntuació Z del 4t estudiant es pot calcular utilitzant la fórmula anterior com,

Z = (x - x) / s

• Z = (65 –30) / 13,44
• Z = -0,47

Per tant, la puntuació del 4t estudiant és de 0,47 desviació estàndard per sota de la puntuació mitjana de la classe, el que significa que el 31,92% de la classe (10 estudiants) va obtenir menys que el 4t estudiant segons la taula de puntuació z.

Puntuació Z a Excel (amb plantilla Excel)

Ara, prenguem el cas esmentat a l’exemple 2 per il·lustrar el concepte de puntuació z a la plantilla excel següent.

A continuació es proporcionen dades per al càlcul de la puntuació Z

Podeu consultar el full d’excel donat a continuació per al càlcul detallat de les estadístiques de la prova de fórmules de puntuació Z.

Rellevància i usos

Des de la perspectiva de la prova d’hipòtesis, la puntuació z és un concepte molt important a entendre, ja que s’utilitza per comprovar si una estadística de prova cau o no en l’interval de valor acceptable. La puntuació z també s'utilitza per estandarditzar les dades abans de l'anàlisi, calcular la probabilitat d'una puntuació o comparar dos o més punts de dades que provenen de distribucions normals diferents. Hi ha una aplicació diversa de la puntuació z en diversos camps si s’aplica correctament.