photosdematures.com

Fórmula per calcular el PV d'una anualitat

El valor actual de la fórmula de la renda vitalícia es calcula determinant el valor actual que es calcula mitjançant els pagaments de les anualitats durant el període de temps dividit per un més la taxa de descompte i el valor actual de la renda vitalícia es determina multiplicant els pagaments mensuals equiparats per un menys el valor actual dividit pels descomptes. taxa.

PV d'una renda anual = C x [(1 - (1 + i) -n) / i]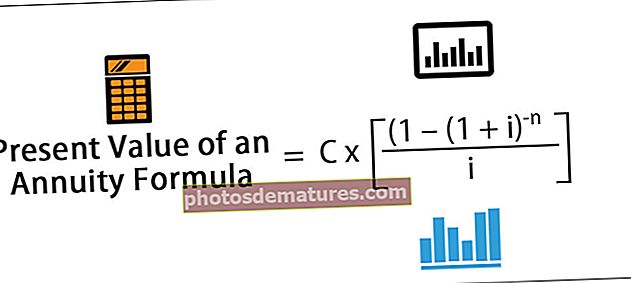

On,

• C és el flux de caixa per període
• i és el tipus d'interès
• n és la freqüència de pagaments

Explicació

La fórmula PV determinarà en un període determinat, el valor actual de diversos pagaments futurs a temps. La fórmula PV de la renda vitalícia es pot veure a partir de la fórmula que depèn del concepte de valor horari dels diners, en què la quantitat de diners d’un dia en el dia actual és més digna que el mateix dòlar que s’haurà de vèncer en una data que sigui passarà en el futur. A més, el PV de la fórmula de la renda s’encarrega de la freqüència de pagament, ja sigui anual, semestral, mensual, etc.

Exemples

Podeu descarregar aquesta plantilla Excel de la fórmula Valor actual de la renda anual - Plantilla Excel de la fórmula Valor actual de la renda anual

Exemple 1

Suposem que hi ha un pagament de la renda de 1.000 dòlars per als pròxims 25 anys a partir de cada final de l'any. Haureu de calcular el valor actual de la renda vitalícia, suposant que el tipus d’interès sigui del 5%.

Solució:

Aquí les anualitats comencen al final de l'any i, per tant, n serà de 25, C és de 1.000 dòlars per als propers 25 anys i i del 5%.

Utilitzeu les dades següents per al càlcul del PV d’una anualitat.

Per tant, el càlcul del PV d’una anualitat es pot fer de la següent manera:

El valor actual de la renda serà -

= 1.000 dòlars x [(1 - (1 + 5%) - 25) / 0,05]

Valor actual d’una renda anual = 14.093,94

Exemple 2

JActualment, ohn treballa en un MNC on se li paguen 10.000 dòlars anuals. En la seva indemnització, hi ha una part del 25% que pagarà una anualitat per part de la companyia. Aquests diners es dipositen dues vegades l'any, a partir de l'1 de juliol i el segon s'ha de vèncer l'1 de gener i continuarà fins als propers 30 anys i, en el moment del rescat, estaria exempta d'impostos.

En el moment de la seva incorporació, també se li va donar una opció per aconseguir 60.000 dòlars alhora, però això estaria subjecte a impostos al tipus del 40%. Haureu d’avaluar si John hauria d’emportar-se els diners ara o esperar fins a 30 anys per rebre el mateix suposant que no compleix els requisits de fons i que la taxa lliure de risc al mercat és del 6%.

Solució

Aquí, les anualitats comencen al final del semestral i, per tant, n serà de 60 (30 * 2), C és de 1.250 $ (10.000 $ * 25% / 2) durant els propers 30 anys i el 2,5% (5% / 2) ).

Utilitzeu les dades següents per al càlcul del valor actual d’una anualitat.

Per tant, el càlcul del valor actual (PV) d’una fórmula de renda es pot fer de la següent manera:

El valor actual de la renda serà -

= 1.250 $ x [(1 - (1 + 2,5%) - 60) / 0,025]

Valor actual d’una renda = 38.635,82 dòlars

Per tant, si John opta per la renda vitalicia, rebria 38.635,82 dòlars.

La segona opció és que opti per 60.000 dòlars, que és abans d’impostos i, si deduïm un impost del 40%, l’import que hi haurà serà de 36.000 dòlars.

 Per tant, John hauria d’optar per la renda vitalícia ja que hi ha un benefici per 2.635,82 dòlars

Exemple 3

A la senyora Carmella s’ofereixen dos productes de jubilació diferents, ja que s’acosta a la jubilació. Tots dos productes començaran el seu flux de caixa a l'edat de 60 anys i continuaran amb anualitats fins als 80 anys. A continuació es detallen els productes. Heu de calcular el valor actual de la renda vital i informar quin és el millor producte per a la senyora Carmella?

Assumeixi un tipus d'interès del 7%.

1) Producte X

Import de la renda = 2.500 dòlars per període. Freqüència de pagament = Trimestral. El pagament es realitzarà al començament del període

2) Producte Y

Import de la renda = 5.150 per període. Freqüència de pagament = semestralment. El pagament es realitzarà al final del període

Atès,

Solució:

Aquí, les anualitats del producte x comencen al començament del trimestre i, per tant, n seran 79, ja que el pagament es fa al començament de la anualitat (20 * 4 menys 1), C és de 2.500 $ durant els propers 20 anys i 1,75% (7% / 4).

Per tant, el càlcul del valor actual d’una anualitat per a un producte X es pot fer de la següent manera:

Valor actual d’una anualitat per al producte X serà -

= 2.500 $ x [(1 - (1 + 1,75%) - 79) / 0,0175]

Valor actual de la renda = 106.575,83 dòlars

Ara hem d’afegir 2.500 dòlars al valor actual superior al fet que es va rebre al començament del període i, per tant, l’import total serà de 1.09.075,83

La segona opció paga semestralment, per tant, n serà 40 (20 * 2), seré del 3,50% (7% / 2) i C és de 5.150 $.

Per tant, el càlcul del PV d’una anualitat per a un producte Y es pot fer de la següent manera:

El valor actual de la renda per al producte Y serà -

= 5.150 $ x [(1 - (1 + 3,50%) - 40) / 0,035]

Valor actual de la renda = 109.978,62 dòlars

Només hi ha un excés de 902,79 dòlars en optar per l’opció 2, de manera que la senyora Carmella hauria de seleccionar l'opció 2.

Rellevància i usos

 La fórmula és força important no només en el càlcul de les opcions de jubilació, sinó que també es pot utilitzar per a les sortides d’efectiu en cas de pressupost de capital, on hi pot haver un exemple de lloguer o d’interessos periòdics pagats que són majoritàriament estàtics, per la qual cosa es utilitzant aquesta fórmula de renda. A més, s’ha de ser prudent mentre s’utilitza la fórmula, ja que cal determinar si els pagaments es fan al començament del període o al final del període, ja que el mateix pot afectar els valors dels fluxos d’efectiu a causa d’efectes de composició.