Distribució de Poisson a Excel

La distribució de Poisson és un tipus de distribució que s’utilitza per calcular la freqüència d’esdeveniments que es produiran en qualsevol moment fix, però els esdeveniments són independents, a Excel 2007 o anteriors teníem una funció incorporada per calcular la distribució de Poisson, per a versions anteriors El 2007 la funció és substituïda per la funció Poisson.DIst.

Sintaxi

X: Aquest és el nombre d'esdeveniments. Ha de ser> = 0.

Significar: El nombre previst d’esdeveniments. Això també hauria de ser> = 0.

Acumulatiu: Això decidirà el tipus de distribució que es vol calcular. Aquí tenim dues opcions CERT o FALS.

TRUE indica la probabilitat que es produeixin un nombre d'esdeveniments entre zero i x.
FALS indica la probabilitat que el nombre d'esdeveniments succeeixi exactament igual que la x.

Exemples

Podeu descarregar aquesta plantilla Poisson Distribution Excel aquí: plantilla Poisson Distribution Excel

Exemple 1

Com a propietari d’una empresa de lloguer de cotxes, els vostres clients mitjans de lloguer de vehicles el cap de setmana són 500. Espereu 520 clients el proper cap de setmana.

Voleu saber el percentatge de probabilitats que es produeixi aquest esdeveniment la setmana vinent.

Pas 1: Aquí x és 520 i el significar és 500. Introduïu aquests detalls a Excel.

Pas 2: Obriu la funció POISSON.DIST en qualsevol de les cel·les.

Pas 3: Seleccioneu el fitxer x argument com a cel·la B1.

Pas 4: L’argument Selecciona mitjana com a cel·la B2.

Pas 5: Estem veient la "funció de distribució acumulativa", així que seleccioneu TRUE com a opció.

Pas 6: Per tant, obtenim el resultat com a 0,82070. Ara, a la cel·la següent, apliqueu la fórmula com a 1 - B5.

Per tant, la probabilitat d’augmentar els clients de lloguer de vehicles de 500 a 520 la propera setmana és d’uns 17,93%.

Exemple 2

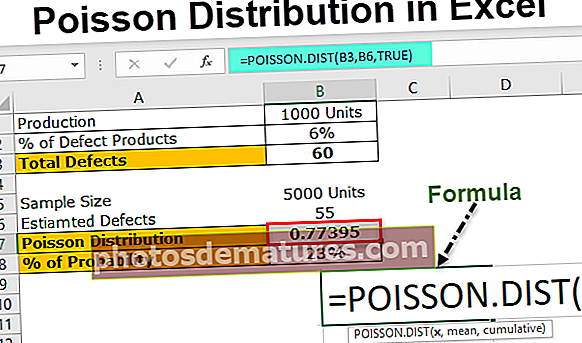
En la producció de 1.000 unitats de productes per a automòbils, el percentatge mitjà de productes amb defectes és d’aproximadament el 6%. De la mateixa manera, en una mostra de 5.000 productes, quina és la probabilitat de tenir 55 productes defectuosos?

Primer calculeu el nombre de productes defectes en 1000 unitats. és a dir, λ = np. λ = 1000 * 0,06.

Per tant, el nombre total de productes defectuosos en 1.000 unitats és de 60 unitats. Ara tenim el nombre total de defectes (x). Per tant, x = 60.

Ara, per reduir els productes defectuosos de 60 a 55, hem de trobar el percentatge de distribució excel·lent de Poisson.

Per tant, SIGNIFICA = 55, x = 60.

La fórmula anterior ens donarà el valor de distribució de Poisson. A la cel·la següent apliqueu la fórmula 1: distribució de Poisson en excel.

Per tant, la probabilitat de reduir els articles amb defectes de 60 a 55 és del 23% aproximadament.

Coses que cal recordar

Vam obtenir l'error numèric de #NUM! és el subministrat x i mitjana els valors són inferiors a zero.
Aconseguirem #VALOR! Si els arguments no són numèrics.
Si els números proporcionats són decimals o fraccionats, excel·leu arrodonit automàticament al nombre enter més proper.

photosdematures.com