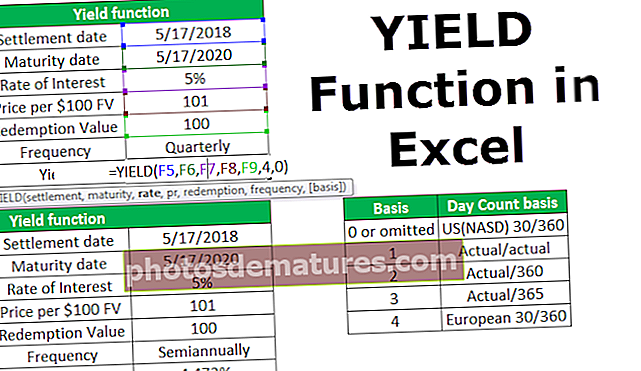
Teorema del límit central (definició, fórmula) | Càlculs i exemples
Definició del teorema del límit central
El teorema del límit central estableix que les mostres aleatòries d’una variable aleatòria de la població amb qualsevol distribució s’acostaran a ser una distribució de probabilitat normal a mesura que augmenta la mida de la mostra i se suposa que a mesura que la mida de la mostra a la població supera els 30, la mitjana de la mostra, que la mitjana de totes les observacions de la mostra s'aproximarà a la mitjana de la població.
Fórmula del teorema del límit central
Ja hem comentat que quan la mida de la mostra supera els 30, la distribució pren la forma d’una distribució normal. Per determinar la distribució normal d’una variable és important conèixer la seva mitjana i la seva variància. Es pot afirmar una distribució normal com
X ~ N (µ, α)
On
- N = nombre d'observacions
- µ = mitjana de les observacions
- α = desviació estàndard
En la majoria dels casos, les observacions no revelen gaire en la seva forma crua. Per tant, és molt important estandarditzar les observacions per poder comparar-les. Es fa amb l'ajut de la puntuació z. Cal calcular la puntuació Z per a una observació. La fórmula per calcular la puntuació z és
Z = (X- µ) / α / √n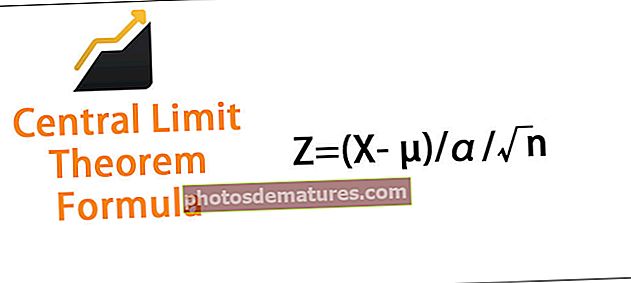
On
- Z = puntuació Z de les observacions
- µ = mitjana de les observacions
- α = desviació estàndard
- n = mida de la mostra
Explicació
El teorema del límit central estableix que les mostres aleatòries d'una variable aleatòria de població amb qualsevol distribució s'aproparan a ser una distribució de probabilitat normal a mesura que augmenta la mida de la mostra. El teorema del límit central suposa que a mesura que la mida de la mostra a la població supera els 30, la mitjana de la mostra que la mitjana de totes les observacions de la mostra serà propera a la mitjana de la població. A més, la desviació estàndard de la mostra quan la mida de la mostra supera els 30 serà igual a la desviació estàndard de la població. Com que la mostra es tria a l'atzar de tota la població i la mida de la mostra és superior a 30, aleshores ajuda a provar hipòtesis i a construir l'interval de confiança per a la prova d'hipòtesis.
Exemples de fórmula del teorema del límit central (amb plantilla d'Excel)
Podeu descarregar aquesta plantilla Excel del formulari del teorema del límit central aquí: plantilla del formulari del formulari del teorema del límit centralExemple 1
Comprenguem el concepte d’una distribució normal amb l’ajut d’un exemple. La rendibilitat mitjana d'un fons d'inversió és del 12% i la desviació estàndard de la rendibilitat mitjana de la inversió en fons d'inversió és del 18%. Si assumim que la distribució de la rendibilitat es distribueix normalment, interpretem la distribució de la rendibilitat en la inversió del fons d'inversió.
Atès,
- La rendibilitat mitjana de la inversió serà del 12%
- La desviació estàndard serà del 18%

Per tant, per esbrinar el retorn d’un interval de confiança del 95%, el podem esbrinar resolent l’equació com

- Rang superior = 12 + 1,96 (18) = 47%
- Rang inferior = 12 - 1,96 (18) = -23%
El resultat significa que el 95% de les vegades que la rendibilitat del fons mutu oscil·larà entre el 47% i el -23%. En aquest exemple, la mida de la mostra, que és el retorn d'una mostra aleatòria de més de 30 observacions de retorn, ens proporcionarà el resultat del retorn de la població del fons d'inversió, ja que la distribució de la mostra es distribuirà normalment.
Exemple 2
Continuant amb el mateix exemple, determinem quin serà el resultat d'un interval de confiança del 90%
Atès,
- La rendibilitat mitjana de la inversió serà del 12%
- La desviació estàndard serà del 18%

Per tant, per esbrinar el retorn d’un interval de confiança del 90%, el podem esbrinar resolent l’equació com

- Rang superior = 12 + 1,65 (18) = 42%
- Rang inferior = 12 - 1,65 (18) = -18%
El resultat significa que el 90% de les vegades que la rendibilitat del fons d'inversió estarà entre el 42% i el -18%.
Exemple 3
Continuant amb el mateix exemple, determinem quin serà el resultat d'un interval de confiança del 99%
Atès,
- La rendibilitat mitjana de la inversió serà del 12%
- La desviació estàndard serà del 18%

Per tant, per esbrinar el retorn d’un interval de confiança del 90%, el podem esbrinar resolent l’equació com

- Rang superior = 12 + 2,58 (18) = 58%
- Rang inferior = 12 - 2,58 (18) = -34%
El resultat significa que el 99% de les vegades que la rendibilitat del fons mutu oscil·larà entre el 58% i el -34%.
Rellevància i ús
El teorema del límit central és extremadament útil ja que permet a l’investigador predir la mitjana i la desviació estàndard de tota la població amb l’ajut de la mostra. Com que la mostra es tria de manera aleatòria de tota la població i la mida de la mostra és superior a 30, llavors qualsevol mida de mostra aleatòria presa de la població s’acostarà a distribuir-se normalment, cosa que ajudarà a provar hipòtesis i a construir l’interval de confiança de la hipòtesi proves. Sobre la base del teorema del límit central, l’investigador és capaç de triar qualsevol mostra aleatòria de tota la població i, quan la mida de la mostra sigui superior a 30, pot predir la població amb l’ajut de la mostra, tal com seguirà la mostra. una distribució normal i també com a mitjana i desviació estàndard de la mostra serà la mateixa que la mitjana i la desviació estàndard de la població.