photosdematures.com

Prova Chi-Square amb Excel

La prova Chi-Square en excel és la prova no paramètrica més utilitzada per comparar dues o més variables per a dades seleccionades aleatòriament. És un tipus de prova que s’utilitza per esbrinar la relació entre dues o més variables, s’utilitza en estadístiques que també es coneix com a valor Chi-quadrat, en excel no tenim una funció incorporada però podem utilitzar fórmules per realitzar la prova chi-quadrat en excel·lència mitjançant la fórmula matemàtica per a la prova Chi-Square.

Tipus

1. Prova Chi-Square per a la bondat de l’ajust
2. Prova Chi-Square per a la independència de dues variables.

# 1: prova Chi-Square per a la bondat de l'ajust

S'utilitza per percebre la proximitat d'una mostra que s'adapta a una població. El símbol de la prova Chi-Square és (2). És la suma de tots els (Recompte observat - Recompte esperat) 2 / Recompte esperat.

• on k-1 graus de llibertat o DF.
• On Oi és la freqüència observada, k és categories, i Ei és la freqüència esperada.

Nota:- La bondat d’ajust d’un model estadístic es refereix a la comprensió de com s’adapten les dades de mostra a un conjunt d’observacions.

Usos

• La solvència dels prestataris segons els grups d’edat i els préstecs personals
• La relació entre el rendiment dels venedors i la formació rebuda
• Rendibilitat d'un sol valor i de valors d'un sector com el farmacèutic o la banca
• Categoria d'espectadors i l'impacte d'una campanya de televisió.

# 2: prova Chi-Square per a la independència de dues variables

S'utilitza per comprovar si les variables són o no autònomes. Amb (r-1) (c-1) graus de llibertat

On Oi és la freqüència observada, r és el nombre de files, c és el nombre de columnes i Ei és la freqüència esperada

Nota:- Dues variables aleatòries s’anomenen independents si la distribució de probabilitat d’una variable no es veu afectada per l’altra.

Usos

La prova d’independència és adequada per a les situacions següents:

• Hi ha una variable categòrica.
• Hi ha dues variables categòriques i haureu de determinar la relació entre elles.
• Hi ha taules creuades i cal trobar la relació entre dues variables categòriques.
• Hi ha variables no quantificables (per exemple, respostes a preguntes com ara, els empleats de diferents grups d’edat trien diferents tipus de plans de salut?)

Com es fa la prova Chi-Square a Excel? (amb exemple)

Podeu descarregar aquesta plantilla Excel de Chi Square Test aquí: plantilla Excel de Chi Square Test

El gerent d’un restaurant vol trobar la relació entre la satisfacció del client i els salaris de les persones que esperen taules. En això, establirem la hipòtesi per provar el Chi-Square

• Agafa una mostra aleatòria de 100 clients preguntant si el servei era excel·lent, bo o deficient.
• A continuació, classifica els sous de les persones que esperen com a baixos, mitjans i alts.
• Suposem que el nivell de significació és 0,05. Aquí, H0 i H1 denoten la independència i la dependència de la qualitat del servei respecte als salaris de les taules d’espera de les persones.
• H₀ - La qualitat del servei no depèn dels salaris de les persones que esperen les taules.
• H₁ - La qualitat del servei depèn dels sous de les persones que esperen les taules
• Les seves conclusions es mostren a la taula següent:

En això, tenim 9 punts de dades, tenim 3 grups, cadascun dels quals ha rebut un missatge diferent sobre el salari i el resultat es dóna a continuació.

Ara comptarem la suma de totes les files i columnes. Ho farem amb l'ajuda de la fórmula, és a dir, SUMA. Per sumar l'excel·lent a la columna total que hem escrit = SUMA (B4: D4) i després premeu Retorn.

Això ens donarà 26. Rendrem el mateix amb totes les files i columnes.

Per calcular el Grau de llibertat (DF) fem servir (r-1) (c-1)

DF = (3-1)(3-1)=2*2=4

• Hi ha 3 categories de serveis i 3 categories de sou
• Tenim 27 enquestats amb un sou mitjà (fila inferior, mitja)
• Tenim 51 enquestats amb un bon servei (última columna, mig)

Ara hem de calcular el Freqüències esperades: -

Freqüències esperades es pot calcular mitjançant una fórmula: -

• Per calcular el Excel · lent utilitzarem multiplicant el total de baix amb el total de Excel·lent dividit per N.

Suposem que hem de calcular la primera fila i la primera columna (= B7 * E4 / B9). Això donarà el nombre esperat de clients que han votat Excel · lent servei per als sous de les persones que esperen com baixa és a dir, 8,32.

• E₁₁₌­­(32*26)/100 = 8.32, E₁₂ = 7.02, E₁₃ = 10.66
• E₂₁ = 16.32, E₂₂ = 13.77, E₂₃ = 20.91
• E₃₁ = 7.36, E₃₂ = 6.21, E₃₃ = 9.41

De la mateixa manera, per a tots, hem de fer el mateix i la fórmula s'aplica al diagrama següent.

Obtenim la taula de freqüències esperades tal com es mostra a continuació: -

Nota:- Suposem que el nivell de significació és 0,05. Aquí, H0 i H1 denoten la independència i la dependència de la qualitat del servei dels salaris de les taules d’espera de les persones.

Després de calcular la freqüència esperada, calcularem els punts de dades chi-quadrat mitjançant una fórmula

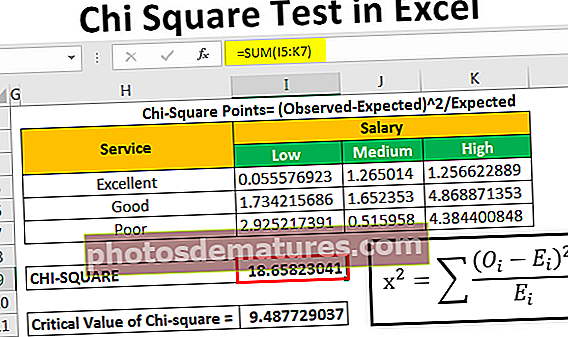
Punts Chi-Quadrat = (Observat-Esperat) ^ 2 / Esperat

Per calcular el primer punt que escrivim = (B4-B14) ^ 2 / B14.

Copiarem i enganxarem la fórmula en altres cel·les per omplir el valor automàticament.

Després d'això, calcularem el valor chi (valor calculat) afegint tots els valors indicats a sobre de la taula

Tenim el valor Chi com 18.65823.

Per calcular el valor crític per a això, fem servir una taula de valors crítics de chi quadrat de la qual podem utilitzar la fórmula que es mostra a continuació.

Aquesta fórmula conté 2 paràmetres CHISQ.INV.RT (probabilitat, grau de llibertat).

Probabilitat és 0,05, és un valor significatiu que ens ajudarà a determinar si acceptem Hipòtesi nul·la (H₀) o no.

El valor crític del chi quadrat és 9.487729037.

Ara trobarem el valor del fitxer chi-quadrat o (valor P)= CHITEST (rang_actual, rang_esperat)

Interval de = CHITEST (B4: D6, B14: D16).

Com hem vist que el valor del test chi o del valor P és = 0,00091723.

Com hem vist que hem calculat tots els valors. El chi quadrat (valor calculat) els valors només són significatius quan el seu valor és igual o superior al valor crític 9,48, és a dir, valor crític (valor tabulat) ha de ser superior a la 18.65 acceptar el Hipòtesi nul·la (H₀).

Però aquí Valor calculat >Valor tabulat

X2 (calculat)> X2 (tabulat)

18.65>9.48

En aquest cas, rebutjarem el fitxer Hipòtesi nul·la (H₀) i Alternatiu (H₁) s’acceptarà.

• També podem utilitzar el valor P per predir el mateix, és a dir, si Valor P <= α (valor significatiu 0,05), es rebutjarà la hipòtesi nul·la
• Si el Valor P> α, no rebutjar el hipòtesi nul · la.

Aquí Valor P (0,0009172)< α (0,05), rebutja H₀, accepteu H₁

A partir de l'exemple anterior, arribem a la conclusió que la qualitat del servei depèn dels salaris de les persones que esperen.

Coses que cal recordar

• Considera el quadrat d’una variada normal estàndard.
• Avalua si les freqüències observades en diferents categories varien significativament de les freqüències esperades en un conjunt especificat de supòsits.
• Determina fins a quin punt una distribució assumida s’adapta a les dades.
• Utilitza taules de contingència (en estudis de mercat, aquestes taules s’anomenen pestanyes creuades).
• Admet mesures a nivell nominal.