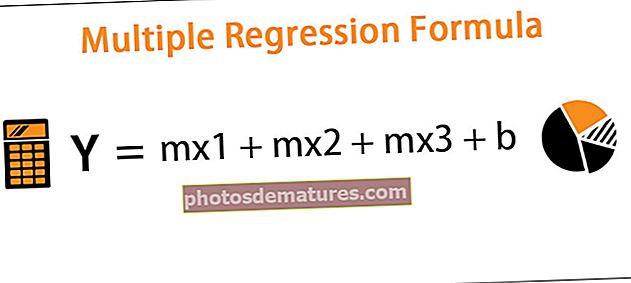Taxa de rendiment nominal (definició, fórmula) | Exemples i càlculs
Quina és la taxa de rendibilitat nominal?
Una taxa de rendibilitat nominal no és altra cosa que la quantitat total de diners que es guanya d’una determinada activitat d’inversió abans d’assumir diverses despeses com assegurances, comissions de gestió, inflació, impostos, honoraris legals, salaris del personal, lloguer d’oficines, depreciació de plantes i maquinària, etc en la deguda consideració. És la rendibilitat bàsica que ofereixen la inversió i la deducció posterior de la inflació i els impostos durant el període d’inversió, la rendibilitat real seria relativament inferior.
Fórmula
La fórmula de la taxa de rendiment nominal es representa de la següent manera: -
Taxa nominal de rendibilitat = Valor de mercat actual - Valor d’inversió original / Valor d’inversió original
Exemples
Exemple 1
Una persona ha fet una inversió de 125.000 dòlars en un fons sense comissions durant un any. Al final de l'any, el valor de la inversió augmenta fins als 130.000 dòlars.
Per tant, la taxa de rendibilitat nominal es pot calcular de la manera següent,

= ($130,000 – $125,000 )/$125,000
Taxa de rendiment nominal = 4%
Mentre es calculen els rendiments de les inversions, es determina la diferència entre la taxa nominal i la rendibilitat real, que s’ajustarà al poder de compra existent. Si la taxa d’inflació prevista és elevada, els inversors esperarien una taxa nominal més elevada.
Cal tenir en compte que aquest concepte pot ser enganyós. Per exemple, és possible que un inversor tingui un bo governamental / municipal i un bo corporatiu que tingui un valor nominal de 1.000 dòlars amb una taxa prevista del 5%. Es podria suposar que els bons tenen el mateix valor. Tanmateix, els bons corporatius solen tributar entre el 25 i el 30% en comparació amb els bons del govern lliures d’impostos. Per tant, la seva taxa de rendiment real és completament diferent.
Exemple 2
Suposem que Andrew compra un CD (certificat de dipòsit) per valor de 150 dòlars a un tipus d’interès anual del 5%. Per tant, els guanys anuals són = 150 $ * 5% = 7,50 $.
D'altra banda, si Andrew inverteix 150 dòlars en un fons d'inversió de renom que també genera una rendibilitat anual del 5%, la rendibilitat anual serà de 7,50 dòlars. No obstant això, un fons d'inversió ofereix un dividend anual de 2,50 dòlars, provocant una diferència en les dues classes d'inversions.
La taula següent us serà útil per entendre les diferències:

(Valor final = Import de la inversió base * Tipus nominal)
- Any 1 = 2,50 * (0,625 / 16,5) = 9,50%
- Any 2 = 2,50 * (0,625 / 18) = 8,70%
- Any 3 = 2,50 * (0,625 / 19,3) = 8,10%
- Any 4 = 2,50 * (0,625 / 20) = 7,80%
- Any 5 = 3,00 * (0,750 / 21) = 10,70%
Com que el fons d'inversió també ofereix un dividend, el dividend trimestral es calcula i es multiplica amb el preu de les accions per calcular la taxa de rendibilitat nominal.

Cal assenyalar que, malgrat que les dues oportunitats d’inversió ofereixen una taxa de rendibilitat idèntica, però factors com els dividends, en aquest cas, tenen un impacte directe sobre la taxa de rendibilitat nominal que s’ofereix.
L'exemple anterior també té en compte el canvi de dividend i l'impacte directe que té sobre el tipus nominal.
Tipus d’interès real vs nominal
Els economistes fan un ús extensiu dels tipus d’interès reals i nominals mentre avaluen el valor de les inversions. De fet, el tipus real utilitza el tipus d’interès nominal com a base a partir de la qual es redueix l’impacte de la inflació:
Tipus d’interès real = Tipus d’interès nominal: inflació
No obstant això, hi ha certes diferències en ambdós conceptes:
| Tipus d’interès real | Tipus d’interès nominal | |
| S'ajusta per eliminar l'impacte de la inflació, reflectint el cost real dels fons per al prestatari i el rendiment real per als inversors. | No té en compte l'impacte de la inflació. | |
| Ofereix una idea clara de la velocitat a la qual augmenta o disminueix el seu poder adquisitiu. | El banc central fixa els tipus a curt termini. El poden mantenir baix per animar els clients a assumir més deutes i augmentar la despesa. | |
| Es pot estimar comparant la diferència entre els rendiments dels bons del tresor i els valors protegits contra la inflació del mateix venciment. | La taxa es cotitza en préstecs i bons. |
Com es calculen els tipus d'interès reals a partir del tipus d'interès nominal?
Aquest exercici pot ser molt útil per comprendre l'impacte de factors econòmics com la inflació i els impostos. A més, des de la perspectiva de diverses inversions, és possible que vulgueu saber quant es preveu que produeixi un dòlar invertit en el futur.
Suposem que Archie té actualment 25 anys i té un pla per jubilar-se als 65 anys (a partir dels 40 anys). Espera acumular al voltant de 2.500.000 dòlars en dòlars actuals en el moment de la seva jubilació. Si pot obtenir un rendiment nominal del 9% anual de les seves inversions i esperar una taxa d’inflació al voltant del 3% anual, quant ha de ser la seva inversió anual per assolir l’objectiu?
La relació entre els tipus d'interès nominal i real és una mica complexa i, per tant, la relació és multiplicativa i no additiva. Per tant, l’equació de Fisher és útil:
Tipus d’interès real (Rr) = ((1 + Rn) / (1 + Ri) - 1)
Per tant, Rn = taxa d’inflació nominal i Ri = taxa d’inflació

Així, Rr = (1+0.09) /(1+0.03) –
1.0582 – 1 = 0.0582 = 5.83%
La inversió anual que utilitza la fórmula del valor futur de la renda

Això significa que si Archie estalvia 16.899.524 $ (en dòlars d’avui) cada any durant els propers 40 anys, tindria 2.500.000 $ al final del mandat.
Vegem aquest problema al revés. Hem d’establir el valor actual de 2.500.000 dòlars en el seu valor actual mitjançant la fórmula del valor futur:

FV = 2.500.000 (1,03) 40 = 2.500.000 * 3,2620
VF = 8.155.094,48 dòlars
Això significa que Archie haurà d’acumular més de 8,15 mm de dòlars (taxa nominal) en el moment de la jubilació per assolir l’objectiu. Això es resoldrà a més utilitzant la mateixa fórmula de FV de renda vitalícia assumint una taxa nominal del 8%:

Per tant, si Archie invertís una quantitat de 31.479,982 $, l'objectiu s'aconseguirà.
Cal assenyalar aquí que les solucions són equivalents, però hi ha una diferència a causa de l'ajust de la inflació cada any. Per tant, se’ns exigeix que creixem cada pagament a un ritme d’inflació.
La solució nominal requereix una inversió de 31.480,77 dòlars, mentre que el tipus d’interès real després d’acomodar la inflació requereix una inversió de 16.878,40 dòlars, que és un escenari més realista.