photosdematures.com

Definició d'EWMA (mitjana mòbil ponderada exponencialment)

La mitjana mòbil ponderada exponencialment (EWMA) es refereix a una mitjana de dades que s’utilitza per fer un seguiment del moviment de la cartera comprovant els resultats i la producció tenint en compte els diferents factors, donant-los els pesos i seguint els resultats per avaluar el rendiment i fer millores

El pes per a una EWMA es redueix de manera exponencial per a cada període que va més enllà en el passat. A més, atès que EWMA conté la mitjana calculada anteriorment, per tant, el resultat de la mitjana mòbil ponderada exponencialment serà acumulatiu. Per això, tots els punts de dades contribuiran al resultat, però el factor de contribució baixarà a mesura que es calculi el pròxim període EWMA.

Explicació

Aquesta fórmula EWMA mostra el valor de la mitjana mòbil en un moment t.

EWMA (t) = a * x (t) + (1-a) * EWMA (t-1)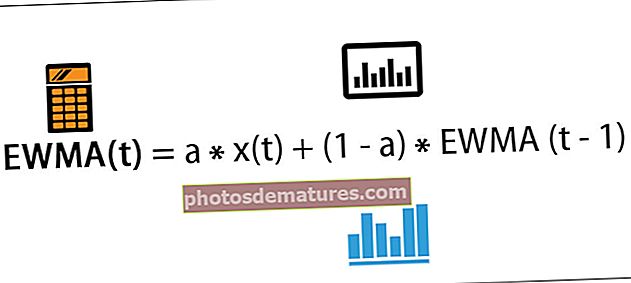

On

• EWMA (t) = mitjana mòbil en el moment t
• a = valor del paràmetre de grau de barreja entre 0 i 1
• x (t) = valor del senyal x en el moment t

Aquesta fórmula estableix el valor de la mitjana mòbil en el moment t. A continuació, es mostra un paràmetre que mostra la velocitat amb què es calcularan les dades més antigues. El valor de a estarà entre 0 i 1.

Si a = 1 significa que només s'han utilitzat les dades més recents per mesurar EWMA. Si a s'aproxima a 0, això significa que es dóna més ponderació a les dades més antigues i si a és a prop d'1, significa que a les dades més recents se li ha donat més ponderació.

Exemples d'EWMA

A continuació es mostren els exemples de mitjana mòbil ponderada exponencialment

Podeu descarregar aquesta plantilla EWMA Excel aquí: plantilla EWMA Excel

Exemple 1

Considerem cinc punts de dades segons la taula següent:

I paràmetre a = 30% o 0,3

Per tant, EWMA (1) = 40

EWMA per al temps 2 és el següent

• EWMA (2) = 0,3 * 45 + (1-0,3) * 40,00
• = 41.5

Calculeu de la mateixa manera la mitjana mòbil ponderada exponencialment per a temps determinats -

• EWMA (3) = 0,3 * 43 + (1-0,3) * 41,5 = 41,95
• EWMA (4) = 0,3 * 31 + (1-0,3) * 41,95 = 38,67
• EWMA (5) = 0,3 * 20 + (1-0,3) * 38,67 = 33,07

Exemple 2

Tenim la temperatura d’una ciutat en graus centígrads de diumenge a dissabte. Utilitzant un = 10% trobarem la mitjana mòbil de temperatura per a cada dia de la setmana.

Utilitzant a = 10% trobarem una mitjana mòbil ponderada exponencialment per a cada dia a la taula següent:

A continuació es mostra el gràfic que mostra una comparació entre la temperatura real i EWMA:

Com podem veure, el suavitzat és força fort fent servir = 10%. De la mateixa manera que podem resoldre la mitjana mòbil ponderada exponencialment per a molts tipus de sèries temporals o conjunts de dades seqüencials.

Avantatges

• Es pot utilitzar per trobar la mitjana mitjançant un historial sencer de dades o de sortida. La resta de gràfics tendeixen a tractar cada dada de manera individual.
• L'usuari pot donar ponderació a cada punt de dades segons la seva comoditat. Aquest pes es pot canviar per comparar diverses mitjanes.
• EWMA mostra les dades geomètricament. A causa d’això, les dades no s’afecten gaire quan es produeixen valors atípics.
• Cada punt de dades de la mitjana mòbil ponderada exponencialment representa una mitjana mòbil de punts.

Limitacions

• Això només es pot utilitzar quan hi ha disponibles dades contínues durant el període de temps.
• Això només es pot utilitzar quan volem detectar un petit canvi en el procés.
• Aquest mètode es pot utilitzar per calcular la mitjana. El seguiment de la variància requereix que l’usuari utilitzi alguna altra tècnica.

Punts importants

• Les dades per a les quals volem obtenir una mitjana mòbil ponderada exponencialment haurien de ser ordenades per temps.
• Això és molt útil per reduir el soroll en punts de dades de sèries temporals sorolloses que es poden anomenar suaus.
• A cada sortida se li dóna un pes. Com més recent sigui la informació, més pes obtindrà.
• És bastant bo per detectar un canvi més petit, però més lent per detectar el canvi gran.
• Es pot utilitzar quan la mida de la mostra del subgrup és superior a 1.
• Al món real, aquest mètode es pot utilitzar en processos químics i en processos comptables quotidians.
• També es pot utilitzar per mostrar les fluctuacions dels visitants del lloc web els dies de la setmana.

Conclusió

EWMA és una eina per detectar canvis menors en la mitjana del procés limitat. Una mitjana mòbil ponderada exponencialment també s’estudia molt i s’utilitza un model per trobar una mitjana mòbil de dades. També és molt útil per pronosticar la base de l’esdeveniment de dades passades. La mitjana mòbil ponderada exponencialment és una base assumida que les observacions es distribueixen normalment. Està considerant dades anteriors en funció del seu pes. Com que les dades són més antigues, el seu pes per al càlcul baixarà exponencialment.

Els usuaris també poden donar pes a les dades anteriors per esbrinar un conjunt diferent de ponderació basada en EWMA. A causa de les dades visualitzades geomètricament, les dades no es veuen afectades gaire a causa dels valors extrems, de manera que es poden obtenir dades més fluides mitjançant aquest mètode.