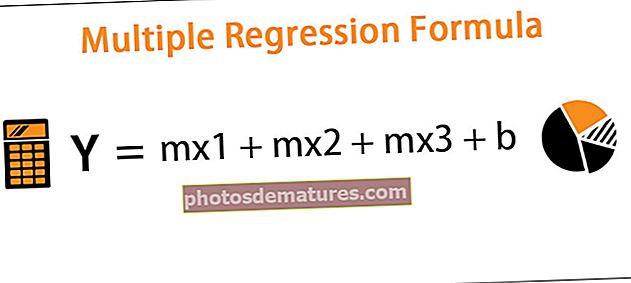Mitjana vs Mitjana ponderada | 4 diferències principals (amb infografies)
La mitjana i la mitjana ponderada són dos termes diferents a Excel, la mitjana és un mètode per calcular el punt central d’un determinat conjunt de dades i es calcula la forma tradicional de calcular la mitjana de sumar els nombres dividits entre el nombre de conjunts de dades presents, mentre que la mitjana ponderada és una mitjana que es calcula de la mateixa manera però amb un pes multiplicat amb cada conjunt de dades.
Diferència entre la mitjana i la mitjana ponderada
La mitjana vs la mitjana ponderada és el terme matemàtic i estadístic en finances i en empreses, però tots dos es calculen de manera diferent. La mitjana és la suma de totes les observacions individuals dividida pel nombre d'observacions. Bàsicament mitjana que s’utilitza per trobar el valor mitjà d’un conjunt de dades concret. També es coneix com a tendència central i s’utilitza per trobar la tendència central d’un grup de dades en un determinat grup de dades. La mitjana ponderada s’utilitza en el camp de la comptabilitat. I el seu propòsit principal és trobar el pes o el valor adequat per resoldre. La mitjana ponderada és el valor de la devolució del principal de determinats bons o préstecs fins que es paga el valor del principal.
Què és la mitjana?
La mitjana és la suma de totes les observacions individuals dividida pel nombre d'observacions. Bàsicament, s’utilitza per trobar valor mitjà en un conjunt de dades concret. També es coneix com a tendència central i s’utilitza per trobar la tendència central d’un grup de dades en un determinat grup de dades. S'utilitza principalment per a la representació de dades. Es pot resoldre per a un conjunt de dades mitjançant la fórmula aritmètica.
Fórmula mitjana = Suma d’observació / Nombre d’observació
Exemple de mitjana
Vegem un exemple per entendre la mitjana.
Suposem que hi ha 10 estudiants a la classe amb les notes 50, 60, 70, 80, 65, 78, 95, 63, 58, 91 respectivament de cada 100, ara anem a trobar la mitjana de les notes superiors d’un estudiant. Com sabem.
Fórmula mitjana = Suma d’observació / Nombre d’observació
Suma d’observació = 50 + 60 + 70 + 80 + 65 + 78 + 95 + 63 + 58 + 9
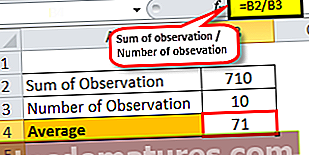
Per tant, la mitjana de la classe de 10 estudiants és de 71.

Quina és la mitjana ponderada?
La mitjana ponderada s’utilitza en el camp de la comptabilitat. El seu propòsit principal és trobar el pes o el valor adequat per resoldre. La mitjana ponderada és el valor de la devolució del principal de determinats bons o préstecs fins que es paga el valor del principal. La mitjana ponderada també és un tipus de mitjana amb una petita diferència, ja que tota observació no porta pesos iguals. Les diferents observacions tenen una importància diferent, cada observació es multiplica pel pes i se suma. La mitjana de pes s’utilitza per realitzar. Es pot prendre com una mitjana en què cada valor té un pes diferent. I està influït pel pes del valor de les dades. El valor ponderat és la suma del producte d'observació en pes dividit per la suma del pes i es pot escriure com:
Fórmula mitjana ponderada = (a1w1 + a2w2 + a3w3 + ... + anwn) / (w1 + w2 + w3 ... + wn)
Exemple de mitjana ponderada
Vegem un exemple per entendre-ho millor.
Suposem que hi ha tres exàmens diferents que contribueixen a obtenir les notes finals per a un any i hi ha el pes diferent de cada examen per al pes del primer examen era del 15%, per al pes del segon examen era del 25% i per al pes de l’examen final era del 60%, ara suposem un estudiant ha obtingut 60 notes en el primer examen, 70 en el segon examen i 80 en l’examen final sobre 100, ara calculem les notes finals d’un estudiant.
Utilitzeu la fórmula esmentada per al seu càlcul.
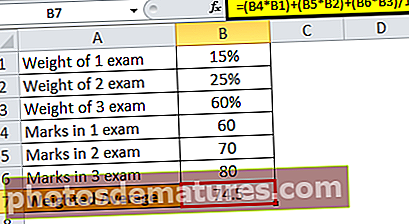
- Per tant, la mitjana ponderada d’un estudiant és de 74,5.
Infografia mitjana vs mitjana ponderada
Aquí us proporcionem les 5 diferències principals.
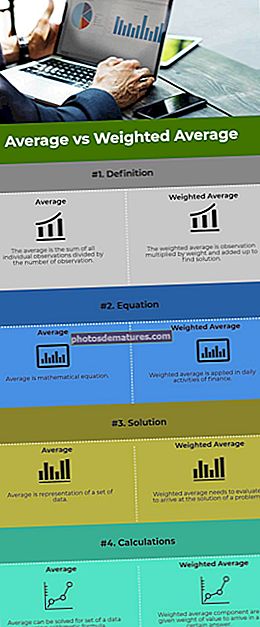
Mitjana vs Mitjana ponderada: diferències clau
Les diferències clau entre aquesta mitjana són les següents:
- La mitjana és la suma de totes les observacions individuals dividides pel nombre d'observacions, mentre que la mitjana ponderada és l'observació multiplicada pel pes i sumada per trobar una solució.
- Una mitjana és una equació matemàtica, mentre que la mitjana ponderada s'aplica a les activitats diàries de finançament.
- La mitjana és la representació d’un conjunt de dades, mentre que la mitjana ponderada s’ha d’avaluar per arribar a la solució d’un problema.
- La mitjana es pot resoldre per al conjunt de dades mitjançant la fórmula aritmètica i es dóna al component mitjà ponderat el pes del valor per arribar a una resposta determinada.
Mitjana vs Diferència mitjana ponderada
Vegem ara les diferències cap a cap.
| Bases | Mitjana | Mitjana ponderada | ||
| Definició | És la suma de totes les observacions individuals dividides pel nombre d'observacions. | És l'observació multiplicada pel pes i sumada per trobar una solució. | ||
| Equació | És una equació matemàtica. | S’aplica a les activitats diàries de finances. | ||
| Solució | És una representació d’un conjunt de dades. | Cal avaluar per arribar a la solució d’un problema. | ||
| Càlculs | Es pot resoldre per a un conjunt de dades mitjançant la fórmula aritmètica. | Es dóna al component el pes del valor per arribar a una resposta determinada. |
Conclusió
Per tant, hem vist la mitjana ponderada i la mitjana ponderada i hem vist la diferència entre ambdues. Hem vist que la mitjana és la suma de totes les observacions individuals dividida pel nombre d’observació i que la mitjana es pot resoldre per a un conjunt de dades mitjançant la fórmula aritmètica, mentre que la mitjana ponderada és l’observació multiplicada per un pes i sumada per trobar un a la solució i al component mitjà ponderat se’ls dóna un pes de valor per arribar a una resposta determinada. Tots dos tenen usuaris diferents segons el problema i es calculen de manera diferent. L’objectiu principal de la mitjana ponderada és trobar el pes o el valor adequat per resoldre. La mitjana ponderada és el valor mitjà de la devolució del principal de determinats bons o préstecs fins que es paga el valor del principal. I la mitjana s’utilitza per trobar el valor mitjà o el valor mitjà.