photosdematures.com

Què és R quadrat ajustat?

L’ajust R quadrat es refereix a l’eina estadística que ajuda els inversors a mesurar l’abast de la variància de la variable dependent que es pot explicar amb la variable independent i considera l’impacte només de les variables independents que tenen un impacte en la variació de la variable dependent.

R ajustat al quadrat o modificat R ^ 2 determina l'abast de la variància de la variable dependent que pot explicar-se mitjançant la variable independent. L’especialitat de la R ^ 2 modificada és que no té en compte l’impacte de totes les variables independents, sinó només aquelles que afecten la variació de la variable dependent. El valor del R ^ 2 modificat també pot ser negatiu, tot i que no és negatiu la major part del temps.

Fórmula quadrada R ajustada

La fórmula per calcular el quadrat R de regressió ajustat es representa a continuació,

R ^ 2 = {(1 / N) * Σ [(xi - x) * (yi - y)] / (σx * σy)} ^ 2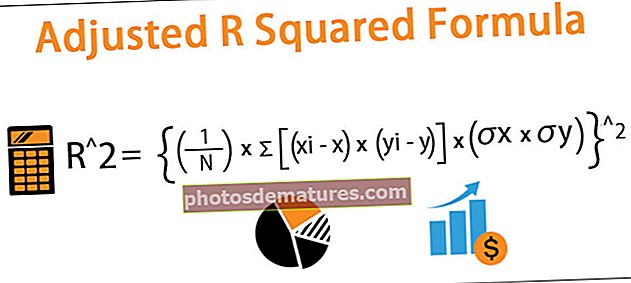

On

• R ^ 2 = quadrat R ajustat de l'equació de regressió
• N = Nombre d'observacions a l'equació de regressió
• Xi = Variable independent de l'equació de regressió
• X = Mitjana de la variable independent de l'equació de regressió
• Yi = Variable dependent de l'equació de regressió
• Y = Mitjana de la variable dependent de l'equació de regressió
• σx = Desviació estàndard de la variable independent
• σy = Desviació estàndard de la variable dependent.

Tingueu en compte

Per calcular-lo a Excel, cal proporcionar variables y i x a Excel i tota la sortida juntament amb R ^ 2 ajustat la genera Excel. És un cas especial en què és difícil proporcionar la sortida en format de text, a diferència d'altres fórmules.

Interpretació

El quadrat R ajustat determina l’extensió de la variància de la variable dependent que es pot explicar per la variable independent. Observant el valor R ^ 2 ajustat, es pot jutjar si les dades de l’equació de regressió són adequades. Com més gran sigui el R ^ 2 ajustat, millor serà l'equació de regressió, ja que implica que la variable independent escollida per determinar la variable dependent és capaç d'explicar la variació de la variable dependent.

El valor del R ^ 2 modificat també pot ser negatiu, tot i que no és negatiu la major part del temps. En el cas del quadrat R ajustat, el valor del quadrat R ajustat augmentarà amb l'addició d'una variable independent només quan la variació de la variable independent impacti la variació de la variable dependent. Això no és aplicable en el cas de R ^ 2, només s'aplica al valor de R ^ 2 ajustat.

Exemples

Podeu descarregar aquesta plantilla Excel de fórmula quadrada R ajustada aquí: plantilla Excel de fórmula quadrada R ajustada

Exemple 1

Intentem comprendre el concepte de R ^ 2 ajustat amb l'ajut d'un exemple. Intentem esbrinar quina relació hi ha entre la distància que recorre el conductor del camió i l'edat del conductor del camió. Algú realment fa una equació de regressió per validar si el que pensa sobre la relació entre dues variables també es valida amb l’equació de regressió.

En aquest exemple concret, veurem quina variable és la variable dependent i quina variable és la variable independent. La variable dependent d'aquesta equació de regressió és la distància que recorre el conductor del camió i la variable independent és l'edat del conductor del camió. En executar una regressió amb les variables, vam aconseguir que el quadrat R ajustat fos del 65%. La instantània següent mostra la sortida de regressió de les variables. El conjunt de dades i les variables es presenten al full Excel adjunt.

El valor R ^ 2 ajustat del 65% per a aquesta regressió implica que el 65% de la variació de la variable dependent s’explica per la variable independent. Idealment, un investigador buscarà el coeficient de determinació més proper al 100%.

Exemple 2

Intentem comprendre el concepte de quadrat R ajustat amb l'ajut d'un altre exemple. Intentem esbrinar quina relació hi ha entre l'alçada dels estudiants d'una classe i la qualificació GPA d'aquests estudiants. En aquest exemple concret, veurem quina variable és la variable dependent i quina variable és la variable independent. La variable dependent d’aquesta equació de regressió és el GPA dels estudiants i la variable independent és l’alçada dels estudiants.

En executar una regressió amb les variables, vam aconseguir que el R ^ 2 ajustat fos insignificant o negatiu. La instantània següent mostra la sortida de regressió de les variables. El conjunt de dades i les variables es presenten al full Excel adjunt.

El valor ajustat de R ^ 2 és insignificant per a aquesta regressió, la qual cosa implica que la variació de la variable dependent no s'explica per la variable independent. Idealment, un investigador buscarà el coeficient de determinació més proper al 100%.

Interpretació

El quadrat R ajustat és una sortida molt important per esbrinar si el conjunt de dades s’ajusta o no. Algú realment fa una equació de regressió per validar si allò que pensa sobre la relació entre dues variables també el valida l’equació de regressió. Com més gran sigui el valor, millor serà l’equació de regressió, ja que implica que la variable independent triada per determinar la variable dependent s’escull correctament. Idealment, un investigador buscarà el coeficient de determinació més proper al 100%.