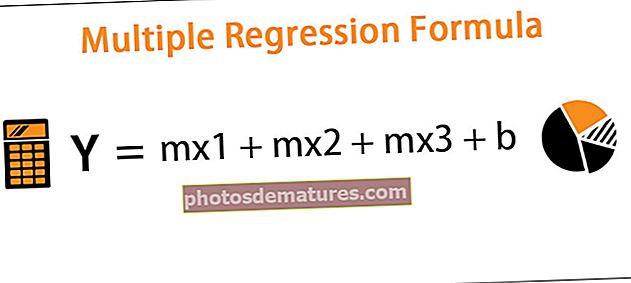photosdematures.com

Què és el coeficient de correlació?

El coeficient de correlació s’utilitza per determinar la intensitat de la relació entre dues variables i els seus valors poden oscil·lar entre -1,0 i 1,0, on -1,0 representa una correlació negativa i +1,0 representa una relació positiva. Considera els moviments relatius de les variables i després defineix si hi ha alguna relació entre elles.

Fórmula del coeficient de correlació

On

• r = coeficient de correlació
• n = nombre d'observacions
• x = 1a variable en el context
• y = 2a variable

Explicació

Si hi ha alguna correlació o es diu la relació entre dues variables, s'indicarà si una de les variables canvia de valor, llavors l'altra variable també tendirà a canviar de valor, per exemple, que pot ser en la mateixa direcció o en sentit contrari. . La part numeradora de l'equació realitza una prova i la força relativa de les variables que es mouen juntes i la part denominadora de l'equació escala el numerador multiplicant les diferències de les variables a partir de variables quadrades.

Exemples

Podeu descarregar aquesta plantilla de fórmula de Excel de coeficient de correlació: plantilla de fórmula de Excel de coeficient de correlació

Exemple 1

Penseu en les dues variables següents x andy, heu de calcular el coeficient de correlació.

A continuació es proporcionen dades per al càlcul

Solució:

Mitjançant l’equació anterior, podem calcular el següent

Tenim tots els valors de la taula anterior amb n = 4.

Introduïu ara els valors per al càlcul del coeficient de correlació.

Per tant, el càlcul és el següent,

r = (4 * 25.032,24) - (262,55 * 317,31) / √ [(4 * 20,855,74) - (262,55) 2] * [(4 * 30,058,55) - (317,31) 2]

r = 16.820,21 / 16.831,57

El coeficient serà -

Coeficient = 0.99932640

Exemple 2

El país X és un país amb economia en creixement i vol fer una anàlisi independent sobre les decisions preses pel seu banc central sobre els canvis en els tipus d’interès si aquests han afectat la inflació i si el banc central pot controlar-lo.

A continuació, es resumeix el resum del tipus d’interès i de la taxa d’inflació que prevalia al país en una mitjana d’aquests anys.

A continuació es proporcionen dades per al càlcul.

El president del país us ha dirigit per fer anàlisis i fer una presentació sobre el mateix en la propera reunió. Utilitzeu la correlació i determineu si el banc central ha complert o no el seu objectiu.

Solució:

Utilitzant la fórmula comentada anteriorment, podem calcular el coeficient de correlació. Tractant la taxa d’interès com una variable, digueu x i tractant la taxa d’inflació com una altra variable com y.

Tenim tots els valors de la taula anterior amb n = 6.

Introduïu ara els valors per al càlcul del coeficient de correlació.

r = (6 * 170,91) - (46,35 * 22,24) / √ [(6 * 361,19) - (46,35) 2] * [(6 * 82,74) - (22,24) 2]

r = -5,36 / 5,88

La correlació serà -

Correlació = -0.92

Anàlisi: Sembla que la correlació entre la taxa d’interès i la taxa d’inflació és negativa, cosa que sembla ser una relació correcta a mesura que augmenta la taxa d’interès, la inflació disminueix, cosa que significa que tendeixen a moure’s en la direcció oposada entre si i, des de dalt, resulta que el banc central va tenir èxit en implementar la decisió relacionada amb la política de tipus d’interès.

Exemple 3

El laboratori ABC fa investigacions sobre l’alçada i l’edat i volia saber si hi ha alguna relació entre ells. Han reunit una mostra de 1.000 persones per a cadascuna de les categories i han arribat a una alçada mitjana en aquest grup.

A continuació es proporcionen dades per al càlcul del coeficient de correlació.

Haureu de calcular el coeficient de correlació i arribar a la conclusió que si existeix alguna relació.

Solució:

Tractant l'edat com una variable, digueu x i tractant l'alçada (en cm) com una altra variable com y.

Tenim tots els valors de la taula anterior amb n = 6.

Introduïu ara els valors per al càlcul del coeficient de correlació.

r = (6 * 10.137) - (70 * 850) / √ [(6 * 940 - (70) 2] * [(6 * 1.20.834) - (850) 2]

r = 1.322,00 / 1.361,23

La correlació serà -

Correlació = 0.971177099

Rellevància i ús

S'utilitza principalment a les estadístiques per analitzar la força de la relació entre les variables que s'estan considerant i, a més, també mesura si hi ha alguna relació lineal entre els conjunts de dades donats i la seva relació. Una de les mesures habituals que s’utilitzen en correlació és el coeficient de correlació de Pearson.

Si una variable canvia de valor i, junt amb aquesta altra, canvia de valor, entendre aquesta relació és fonamental, ja que es pot utilitzar el valor de la primera variable per predir el canvi en un valor de la segona variable. Una correlació té molts usos actuals en aquesta època moderna, ja que s’utilitza a la indústria financera, la investigació científica i on no. Però, però, és important saber que la correlació té tres tipus principals de relacions. La primera és una relació positiva que afirma que si hi ha un canvi en el valor d’una variable, hi haurà un canvi en la variable relacionada en la mateixa direcció, de manera similar, si hi ha una relació negativa, la variable relacionada es comportarà en direcció oposada. A més, si no hi ha correlació, llavors r implicarà un valor zero. Vegeu les imatges següents per entendre millor el concepte.