photosdematures.com

Què és Kurtosis?

La curtosi a les estadístiques s’utilitza per descriure la distribució del conjunt de dades i mostra fins a quin punt els punts de conjunt de dades d’una distribució particular difereixen de les dades d’una distribució normal. S'utilitza per determinar si una distribució conté valors extrems.

Explicació

A l’àmbit de les finances, s’utilitza per mesurar el volum de risc financer associat a qualsevol instrument o transacció. Més la curtosi és el risc financer associat al conjunt de dades en qüestió. L'asimetria és una mesura de simetria en una distribució mentre que la curtosi és la mesura de la pesadesa o la densitat de les cues de distribució.

Tipus de curtosi

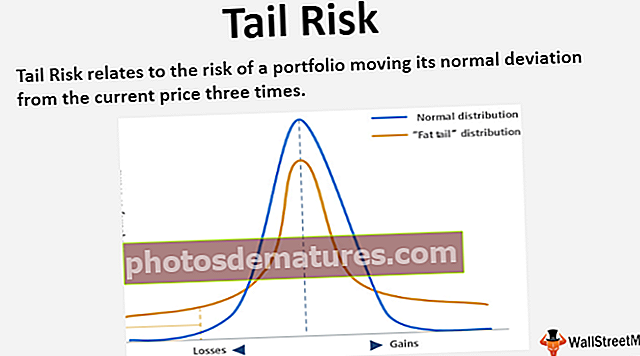
A continuació es mostra la representació pictòrica de la curtosi (els tres tipus, cadascun s’explica detalladament al paràgraf següent)

# 1 - Mesokurtic

Si la cortosi de les dades cau a zero o és igual a zero, es coneix com Mesokurtic. Això significa que el conjunt de dades segueix una distribució normal. La línia blava de la imatge superior representa una distribució mesokúrtica. A les finances, aquest patró mostra el risc a un nivell moderat.

# 2 - Leptocurtic

Quan la curtosi és positiva en altres termes més que zero, les dades cauen en el leptocurtic. Leptokurtic té fortes corbes pronunciades a banda i banda que indiquen la forta població de valors atípics del conjunt de dades. En termes de finançament, una distribució leptocúrtica demostra que el retorn de la inversió pot ser altament volàtil a gran escala a banda i banda. Es diu que una inversió després de la distribució leptocúrtica és una inversió arriscada, però també pot generar rendiments importants per compensar el risc. La corba verda de la imatge superior representa la distribució leptocúrtica.

# 3 - Platykurtic

Sempre que la curtosi és inferior a zero o negativa, es refereix a Platykurtic. El conjunt de distribució segueix la corba subtil o pàl·lida i aquesta corba indica el petit nombre de valors atípics en una distribució. Normalment, els inversors demanen una inversió que cau sota el platiquurtic a causa de la petita probabilitat de generar un retorn extrem. També els petits valors atípics i la cua plana indiquen el menor risc que comporten aquestes inversions. la línia vermella de la representació gràfica anterior representa una distribució platyurtica o una inversió segura.

Importància

• Des de la perspectiva dels inversors, una elevada cortosi de la distribució del retorn implica que una inversió produirà rendiments extrems ocasionals. Això pot fer canviar les dues formes que són o bé rendiments positius de rendiments negatius extrems. Per tant, aquesta inversió comportava un alt risc. Aquest fenomen es coneix com a risc de curtosi. La distinció mesura la mida combinada de les dues cues, la curtosi mesura la distribució entre els valors d’aquestes cues.
• Quan la distribució de la curtosi es calcula sobre qualsevol conjunt de dades d’una inversió concreta, el risc de la inversió contra la probabilitat de generar rendiments. Segons el seu valor i el tipus al qual pertany, els assessors d’inversions poden fer les prediccions d’inversió. Basant-se en les prediccions, els assessors assessoraran l'estratègia i l'agenda d'inversió a l'inversor i escolliran fer la inversió. Per calcular la curtosi en excel, hi ha una funció integrada Kurt en excel.

Avantatges

• Es calcula a partir del conjunt de dades de la inversió, el valor obtingut es pot utilitzar per representar la naturalesa de la inversió. Una major desviació de la mitjana significa que els rendiments també són elevats per a la inversió en particular.
• Quan l'excés de curtosi en pla, significa que la probabilitat de generar un rendiment elevat de la inversió és baixa i generarà rendiments elevats en només uns pocs escenaris, regularment el rendiment no és tan alt de la inversió.
• Un excés de curtosi significa que el retorn de la inversió pot oscil·lar en ambdós sentits. Significa que els rendiments generats poden ser molt elevats o molt baixos segons els valors atípics de la distribució. Quan és negatiu, indica que la desviació del conjunt de dades respecte a la mitjana és plana.

Conclusió

• La curtosi s’utilitza com a mesura per definir el risc que comporta una inversió. La naturalesa de la inversió per generar rendiments més elevats també es pot predir a partir del valor de la curtosi calculada. Com més gran sigui l'excés per a qualsevol conjunt de dades d'inversió, major serà la seva desviació de la mitjana.
• Això significa que aquesta inversió pot generar rendiments més elevats o esgotar el valor de la inversió en major mesura. Un excés de curtosi més proper a zero o una desviació plana de la mitjana mostra que la inversió tindrà una probabilitat menor de generar rendiments elevats. Es pot utilitzar per definir el risc financer de la inversió. Per a l'assessor d'inversions, la curtosi és un factor crucial per definir el risc d'inversió associat a la cartera del fons.