photosdematures.com

Fórmula per calcular la prova Z en estadístiques

La prova Z en estadístiques es refereix a la prova d’hipòtesi que s’utilitza per determinar si les dues mostres calculades són diferents, en cas que hi hagi desviacions estàndard disponibles i la mostra sigui gran.

Z = (x - μ) / ơ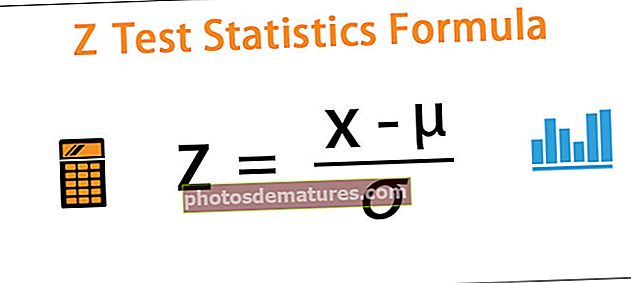

on x = qualsevol valor de la població

• μ = mitjana de població
• ơ = desviació estàndard de la població

En el cas d’una mostra, la fórmula per a les estadístiques de valor de la prova z es calcula deduint la mitjana mostral del valor x i, a continuació, el resultat es divideix per la desviació estàndard de la mostra. Matemàticament, es representa com,

Z = (x - x_mig) / s

on

• x = qualsevol valor de la mostra
• x_means = mitjana mostral
• s = desviació estàndard de la mostra

Càlcul de la prova Z (pas a pas)

La fórmula per a les estadístiques de la prova z per a una població es deriva mitjançant els passos següents:

• Pas 1: En primer lloc, calculeu la mitjana de la població i la desviació estàndard de la població segons l’observació capturada a la mitjana de la població, i cada observació es denota amb x_jo. El nombre total d’observacions a la població es denota amb N.

Mitjana de població,

Desviació estàndard de la població,

• Pas 2: Finalment, les estadístiques de la prova z es calculen deduint la mitjana de la població de la variable i el resultat es divideix per la desviació estàndard de la població, tal com es mostra a continuació.

Z = (x - μ) / ơ

La fórmula per a les estadístiques de la prova z d’una mostra es deriva mitjançant els passos següents:

• Pas 1: En primer lloc, calculeu la mitjana de la mostra i la desviació estàndard de la mostra igual que l'anterior. Aquí, el nombre total d'observacions a la mostra es denota per n tal que n <N.

Mitjana de mostra,

Desviació estàndard de mostra,

• Pas 2: Finalment, les estadístiques de la prova z es calculen deduint la mitjana mostral del valor x i, a continuació, el resultat es divideix per la desviació estàndard de la mostra, tal com es mostra a continuació.

Z = (x - x_mig) / s

Exemples

Podeu descarregar aquesta plantilla de prova de fórmula Excel aquí: plantilla de prova de fórmula Excel de Z

Exemple 1

Suposem que hi ha una població d’alumnes d’una escola que va presentar-se a una prova de classe. La puntuació mitjana a la prova és de 75 i la desviació estàndard és de 15. Determineu la puntuació de la prova z de David que va obtenir 90 a la prova.

Atès,

• La mitjana de la població, μ = 75
• Desviació estàndard de la població, ơ = 15

Per tant, les estadístiques de la prova z es poden calcular com:

Z = (90 - 75) / 15

Les estadístiques de la prova Z seran -

• Z = 1

Per tant, la puntuació de la prova de David és una desviació estàndard per sobre de la puntuació mitjana de la població, és a dir, segons la taula de puntuació z, el 84,13% dels estudiants menys puntuació que David.

Exemple 2

Prenguem l'exemple de 30 estudiants que van ser seleccionats per formar part d'un equip de mostra per ser enquestats per veure quants llapis s'estaven utilitzant en una setmana. Determineu la puntuació de la prova z del tercer alumne a partir de les respostes donades: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Atès,

• x = 5, ja que la resposta del tercer alumne, és 5
• Mida de la mostra, n = 30

Mitjana mostral, = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30

Mitjana = 4,17

Ara, la desviació estàndard de la mostra es pot calcular mitjançant la fórmula anterior.

ơ = 1,90

Per tant, la puntuació de la prova z del tercer estudiant es pot calcular com:

Z = (x - x) / s

• Z = (5 –17) / 1,90
• Z = 0,44

Per tant, l’ús del tercer estudiant és 0,44 vegades la desviació estàndard per sobre de l’ús mitjà de la mostra, és a dir, segons la taula de puntuació z, el 67% dels estudiants utilitzen menys llapis que el tercer estudiant.

Exemple 3

Prenguem l'exemple de 30 estudiants que van ser seleccionats per formar part d'un equip de mostra per ser enquestats per veure quants llapis s'estaven utilitzant en una setmana. Determineu la puntuació de la prova z del tercer alumne a partir de les respostes donades: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

A continuació es proporcionen dades per al càlcul de les estadístiques de prova Z

Podeu consultar el full d’excel donat a continuació per al càlcul detallat de les estadístiques de proves Z.

Rellevància i usos

És molt important entendre el concepte d’estadístiques de la prova z, perquè s’utilitza generalment sempre que es pot discutir si una estadística de prova segueix o no una distribució normal sota la hipòtesi nul·la en qüestió. Tot i això, s’ha de tenir en compte que només s’utilitza una prova z quan la mida de la mostra és superior a 30, en cas contrari s’utilitza la prova t.