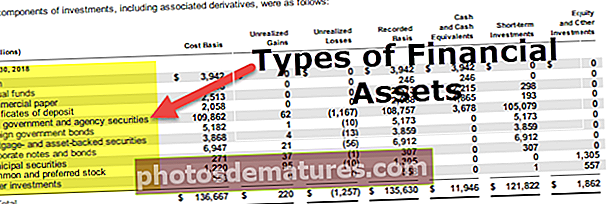
Fórmula del valor P | Exemples pas a pas per calcular el valor P.
Què és la fórmula del valor P?
P és una mesura estadística que ajuda els investigadors a determinar si la seva hipòtesi és correcta. Ajuda a determinar la importància dels resultats. La hipòtesi nul·la és una posició per defecte que no existeix cap relació entre dos fenòmens mesurats. Es denota per H0. Una alternativa la hipòtesi és la que es creuria si es conclou que la hipòtesi nul·la és falsa. El seu símbol és H1 o Ha.
El valor P a Excel és un nombre entre 0 i 1. Hi ha taules, programes de fulls de càlcul i programari estadístic per ajudar a calcular el valor p. El nivell de significació (α) és un llindar predefinit establert per l’investigador. Generalment és de 0,05. Un valor p molt petit, inferior al nivell de significació, indica que rebutgeu la hipòtesi nul·la. El valor P que és superior al nivell de significació indica que no rebutgem la hipòtesi nul·la.
Explicació de la fórmula del valor P.
La fórmula per al càlcul del valor p es pot obtenir seguint els passos següents:
Càlcul del valor P a partir d'una estadística Z
Pas 1: Hem d’esbrinar l’estadística de prova z


On
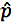 és la proporció de mostra
és la proporció de mostra- p0 és la proporció de població suposada en la hipòtesi nul·la
- n és la mida de la mostra
Pas 2: Hem de trobar el nivell de p corresponent a partir del valor z obtingut. Amb aquest propòsit, hem de mirar la taula z.

Font: www.dummies.com
Per exemple, trobem el valor de p corresponent a z ≥ 2,81. Com que la distribució normal és simètrica, els valors negatius de z són iguals als seus valors positius. 2,81 és una suma de 2,80 i 0,01. Mireu 2.8 a la columna z i el valor corresponent de 0.01. Obtenim p = 0,0025.
Exemples de fórmula de valor P (amb plantilla d'Excel)
Vegem alguns exemples senzills o avançats de l’equació del valor P per entendre-la millor.
Podeu descarregar aquesta plantilla Excel de P Value Formula aquí: plantilla Excel de Formula Value P
Exemple 1
a) El valor P és 0,3015. Si el nivell de significació és del 5%, busqueu si podem rebutjar la hipòtesi nul·la.
b) El valor P és 0,0129. Si el nivell de significació és del 5%, busqueu si podem rebutjar la hipòtesi nul·la.
Solució:
Utilitzeu les dades següents per al càlcul del valor P.

El valor P serà -

a) Com que el valor p de 0,3015 és superior al nivell de significació de 0,05 (5%), no rebutgem la hipòtesi nul·la.
b) Com que el valor p de 0,0129 és inferior al nivell de significació de 0,05, rebutgem la hipòtesi nul·la.
Exemple 2
El 27% de la gent de l'Índia parla hindi segons un estudi de recerca. Un investigador té curiositat per saber si la xifra és més alta al seu poble. Per tant, emmarca la hipòtesi nul·la i alternativa. Posa a prova H0: p = 0,27. Ha: p> 0,27. Aquí, p és la proporció de gent del poble que parla hindi. Encarrega una enquesta al seu poble per esbrinar el nombre de persones que parlen hindi. Troba que 80 de cada 240 persones de la mostra poden parlar hindi. Esbrineu el valor p aproximat per a la prova de l’investigador si suposem que es compleixen les condicions necessàries i que el nivell de significació és del 5%.
Solució:
Utilitzeu les dades següents per al càlcul del valor P.

Aquí, la mida de la mostra n = 240,
pàg0 és la proporció de població Haurem de trobar la proporció de mostra 
= 80 / 240
 = 0.33
= 0.33
Z Estadística
Càlcul de l'estadística Z


=0.33 – 0.27 / √ 0.27 * (1 – 0.27 ) / 240
L'estadística Z serà -

Z = 2.093696
El valor P serà -

Valor P = P (z ≥ 2,09)
Hem de mirar que el valor de 2,09 és la taula z. Per tant, hem de mirar -2,0 a la columna z i el valor a 0,09 columna. Com que la distribució normal és simètrica, l'àrea a la dreta de la corba és igual a la de l'esquerra. Obtenim el valor p com 0,0183.
Valor P = 0.0183
Com que el valor p és inferior al nivell significatiu de 0,05 (5%), rebutgem la hipòtesi nul·la.
Nota: A Excel, el valor p arriba a 0,0181
Exemple 3
Els estudis demostren que els homes compren un major nombre de bitllets de vol en comparació amb les dones. Els compren homes i dones en una proporció de 2: 1. La investigació es va dur a terme en un aeroport concret de l'Índia per trobar la distribució dels bitllets d'avió entre homes i dones. De 150 bitllets, 88 van ser comprats per homes i 62 per dones. Hem d’esbrinar si la manipulació experimental provoca el canvi en els resultats o observem una variació casual. Calculeu el valor p assumint que el grau de significació és 0,05.
Solució:
Utilitzeu les dades següents per al càlcul del valor P.

Pas 1: El valor observat és de 88 per als homes i 62 per a les dones.
- Valor esperat per a homes = 2/3 * 150 = 100 homes
- Valor esperat per a dones = 1/3 * 150 = 50 dones
Pas 2: Esbrineu el chi-quadrat


=((88-100)2)/100 + (62-50) 2/50
=1.44+2.88
Chi-Square (X ^ 2)
Chi-Square (X ^ 2) serà -

Chi-Square (X ^ 2) = 4.32
Pas 3: Cerqueu els graus de llibertat
Com que hi ha 2 variables: homes i dones, n = 2
Graus de llibertat = n-1 = 2-1 =
Pas 4: A la taula del valor p, observem la primera fila de la taula, ja que el grau de llibertat és 1. Podem veure que el valor p està entre 0,025 i 0,05. Com que el valor p és inferior al grau de significació de 0,05, rebutgem la hipòtesi nul·la.
El valor P serà -

Valor P = 0.037666922
Nota: Excel dóna directament el valor p mitjançant la fórmula:
CHITEST (abast real, abast previst)
Exemple # 4
Se sap que el 60% de les persones que entren a les botigues de roba d’una ciutat compren alguna cosa. El propietari d’una botiga de roba volia saber si el nombre de botigues de roba que tenia era més elevat. Ja tenia els resultats d’un estudi realitzat a la seva botiga. 128 de cada 200 persones que van entrar a la seva botiga van comprar alguna cosa. El propietari de la botiga va indicar pas la proporció de persones que van entrar a la seva botiga de roba i van comprar alguna cosa. La hipòtesi nul·la emmarcada per ell era p = 0,60 i la hipòtesi alternativa era p> 0,60. Trobeu el valor p de la investigació en un nivell de significació del 5%.
Solució:
Utilitzeu les dades següents per al càlcul del valor P.

Aquí, la mida de la mostra n = 200. Haurem de trobar la proporció de la mostra
= 128 / 200
 = 0.64
= 0.64
Z Estadística
Càlcul de l'estadística Z


= 0.64 – 0.60 / √ 0.60 * (1 – 0.60) /200
L'estadística Z serà -

Z Estadística =1.1547
Valor P = P (z ≥ 1,1547)
Funció NORMSDIST a Excel

NORMSDIST serà -

NORMSDIST = 0.875893461
Hi ha una funció incorporada per calcular un valor p a partir d’una estadística z a Excel. Es coneix com la funció NORMSDIST. La funció Excel NORMSDIST calcula la funció de distribució acumulativa normal estàndard a partir d’un valor subministrat. El seu format és NORMSDIST (z). Com que el valor estadístic z es troba a la cel·la B2, la funció utilitzada és = NORMSDIST (B2).
El valor P serà -

Valor P = 0.12410654
Com que hem de trobar l'àrea a la dreta de la corba,
valor p = 1 - 0,875893 = 0,1224107
Com que el valor p de 0,1224107 és més que un nivell significatiu de 0,05, no rebutgem la hipòtesi nul·la.
Rellevància i ús
P-Value té aplicacions àmplies en proves d’hipòtesis estadístiques, específicament en proves d’hipòtesis nul·les. Per exemple, una administradora de fons gestiona un fons d'inversió. Afirma que els rendiments d'un esquema particular del fons d'inversió són equivalents a Nifty, que és l'índex borsari de referència. Enquadraria la nul·la hipòtesi que les rendibilitats del pla de fons d'inversió són equivalents a la de Nifty. La hipòtesi alternativa seria que els rendiments de l’esquema i els rendiments Nifty no siguin equivalents. Després calcularia el valor p.

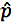 és la proporció de mostra
és la proporció de mostra