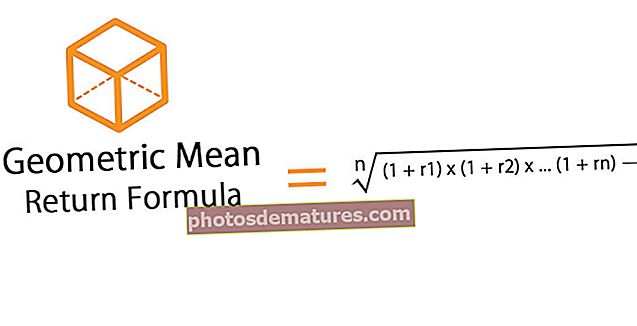Retorn mitjà geomètric (definició, fórmula) | Com es calcula?
Què és el retorn mitjà geomètric?
La rendibilitat mitjana geomètrica calcula la rendibilitat mitjana de les inversions que es compon en funció de la seva freqüència en funció del període de temps i s’utilitza per analitzar el rendiment de la inversió ja que indica la rendibilitat d’una inversió.
Fórmula geomètrica de retorn

- r = taxa de rendiment
- n = nombre de períodes
És el conjunt mitjà de productes definits tècnicament com a productes arrel «n», del nombre esperat de períodes. El focus del càlcul és presentar una "comparació de poma a poma" quan es contemplen 2 tipus similars d'opcions d'inversió.
Exemples
Comprenem la fórmula amb l'ajut d'un exemple:
Podeu descarregar aquesta plantilla Excel de retorn mitjà geomètric aquí: plantilla Excel de retorn mitjà geomètric
Suposant el retorn de 1.000 dòlars en un mercat monetari que guanya un 10% el primer any, un 6% el segon any i un 5% el tercer any, el rendiment mitjà geomètric serà:

Aquest és el rendiment mitjà tenint en compte l’efecte de composició. Si hagués estat un rendiment mitjà simple, hauria pres la suma dels tipus d’interès donats i el dividiria per 3.
Per tant, per arribar al valor de 1.000 dòlars després de 3 anys, la rendibilitat es cobrarà al 6,98% cada any.
Primer any
- Interessos = 1.000 $ * 6,98% = 69,80 $
- Principal = 1.000 $ + 69,80 $ = 1.069,80 $
2n any
- Interessos = 1.069,80 $ * 6,98% = 74,67 $
- Principal = 1.069,80 $ + 74,67 $ = 1.144,47 $
Any 3
- Interessos = 1.144,47 $ * 6,98% = 79,88 $
- Principal = 1.144,47 $ + 79,88 $ = 1.224,35 $
- Per tant, l'import final després de 3 anys serà de 1.224,35 $, que equivaldrà a compondre l'import principal mitjançant els 3 interessos individuals compostos anualment.
Considerem un altre cas per comparar:
Un inversor manté una acció volàtil amb rendibilitats que varien significativament d’un any a l’altre. La inversió inicial va ser de 100 dòlars a l’acció A i va retornar el següent:
Any 1: 15%
Any 2: 160%
Any 3: -30%
Any 4: 20%
- La mitjana aritmètica serà = [15 + 160 - 30 + 20] / 4 = 165/4 = 41,25%
Tanmateix, el veritable retorn serà:
- Any 1 = 100 $ * 15% [1,15] = 15 $ = 100 + 15 = 115 $
- Any 2 = 115 $ * 160% [2,60] = 184 $ = 115 + 184 = 299 $
- Any 3 = 299 $ * -30% [0,70] = 89,70 $ = 299 - 89,70 = 209,30 $
- Any 4 = 209,30 dòlars * 20% [1,20] = 41,86 dòlars = 209,30 + 41,86 = 251,16 dòlars
La mitjana geomètrica resultant, en aquest cas, serà del 25,90%. Això és molt inferior a la mitjana aritmètica del 41,25%
El problema de la mitjana aritmètica és que tendeix a exagerar la rendibilitat mitjana real en una quantitat significativa. En l'exemple anterior, es va observar que en el segon any els rendiments havien augmentat un 160% i després van caure un 30%, que és la variació interanual un 190%.
Per tant, la mitjana aritmètica és fàcil d’utilitzar i calcular i pot ser útil en intentar trobar la mitjana de diversos components. Tanmateix, és una mètrica inadequada que s’ha d’utilitzar per determinar el rendiment mitjà real de la inversió. La mitjana geomètrica és molt útil per mesurar el rendiment d’una cartera.
Usos
Els usos i beneficis de la fórmula de retorn mitjà geomètric són:
- Aquesta rendibilitat s’utilitza específicament per a inversions agregades. Un compte d'interès senzill farà servir la mitjana aritmètica per simplificar-la.
- Es pot utilitzar per desglossar el tipus efectiu per període de retenció.
- S'utilitza per a fórmules de flux de caixa del valor actual i del valor futur.
Calculadora de retorn mitjà geomètric
Podeu utilitzar la Calculadora següent.
| r1 (%) | |
| r2 (%) | |
| r3 (%) | |
| Fórmula geomètrica de retorn = | |
| Fórmula geomètrica de retorn mitjà = 3 √ (1 + r1) * (1 + r2) * (1 + r3) - 1 = |
| 3 √ (1 + 0 ) * (1 + 0 ) * (1 + 0 ) − 1 = 0 |
Fórmula de retorn mitjà geomètric a Excel (amb plantilla Excel)
Fem ara el mateix exemple anterior a Excel. Això és molt senzill. Heu de proporcionar les dues entrades de Taxa de nombres i Nombre de períodes.
Podeu calcular fàcilment la mitjana geomètrica a la plantilla proporcionada.

Per tant, per arribar al valor de 1.000 dòlars després de 3 anys, la rendibilitat es cobrarà al 6,98% cada any.

Per tant, l'import final després de 3 anys serà de 1.224,35 $, que equivaldrà a compondre l'import principal mitjançant els 3 interessos individuals compostos anualment.
Considerem un altre cas per comparar:

Tanmateix, el veritable retorn serà:

La mitjana geomètrica resultant, en aquest cas, serà del 25,90%. Això és molt inferior a la mitjana aritmètica del 41,25%