photosdematures.com

Què és la desviació del quartil?

Desviació del quartil es basa en la diferència entre el primer quartil i el tercer quartil en la distribució de freqüències i la diferència també es coneix com a rang intercuartil, la diferència dividida per dos es coneix com a desviació del quartil o rang semi intercuartil.

Quan es pren la meitat de la diferència o la variància entre el 3r quartil i el 1r quartil d'una distribució simple o distribució de freqüència és la desviació del quartil.

Fórmula

Una fórmula de desviació del quartil (Q.D.) s’utilitza en estadístiques per mesurar la dispersió o, en altres paraules, per mesurar la dispersió. Això també es pot anomenar un rang inter-quartils.

Q.D. = Q3 - Q1 / 2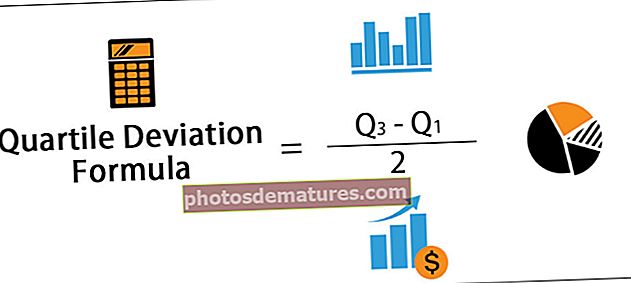

• La fórmula inclou Q3 i Q1 en el càlcul, que és superior al 25% i redueix el 25% de les dades, respectivament, i quan es pren la diferència entre aquests dos i quan aquest nombre es redueix a la meitat, dóna mesures de dispersió o dispersió.
• Per tant, per calcular la desviació del quartil, primer heu d’esbrinar Q1, després el segon pas és trobar Q3 i després prendre una diferència d’ambdós i el pas final és dividir per 2.
• Aquest és un dels millors mètodes de dispersió per a dades de composició oberta.

Exemples

Podeu descarregar aquesta plantilla Excel de la fórmula de desviació del quartil aquí: plantilla Excel de la fórmula de desviació del quartil

Exemple 1

Penseu en un conjunt de dades dels números següents: 22, 12, 14, 7, 18, 16, 11, 15, 12. Heu de calcular la desviació del quartil.

Solució:

En primer lloc, hem d’organitzar les dades en ordre ascendent per trobar Q3 i Q1 i evitar duplicats.

7, 11, 12, 13, 14, 15, 16, 18, 22

El càlcul de Q1 es pot fer de la següent manera,

Q1 = ¼ (9 + 1)

=¼ (10)

P1=2.5 Termini

El càlcul de Q3 es pot fer de la següent manera,

Q3 = ¾ (9 + 1)

=¾ (10)

P3= 7.5 Termini

El càlcul de la desviació del quartil es pot fer de la següent manera,

• Q1 és una mitjana de 2n que és 11 i suma el producte de la diferència entre 3r i 4t i 0,5 que és (12-11) * 0,5 = 11,50.
• Q3 és el 7è trimestre i el producte de 0,5 i la diferència entre el 8è i el 7è trimestre que és (18-16) * 0,5 i el resultat és 16 + 1 = 17.

Q.D. = Q3 - Q1 / 2

Utilitzant la fórmula de desviació del quartil, tenim (17-11.50) / 2

=5.5/2

Q.D.=2.75.

Exemple 2

Harry Ltd. és fabricant de tèxtils i treballa en una estructura de recompensa. La direcció està en debat per iniciar una nova iniciativa, però primer volen saber quant difon la producció.

La direcció ha recollit les seves dades mitjanes de producció diàries dels darrers 10 dies per empleat (mitjà).

155, 169, 188, 150, 177, 145, 140, 190, 175, 156.

Utilitzeu la fórmula de desviació del quartil per ajudar la gestió a trobar la dispersió.

Solució:

El nombre d'observacions aquí és 10 i el nostre primer pas seria organitzar les dades en ordre ascendent.

140, 145, 150, 155, 156, 169, 175, 177, 188, 190

El càlcul de Q1 es pot fer de la següent manera,

Q1 = ¼ (n + 1) tercer terme

=¼ (10+1)

=¼ (11)

P1= 2,75è Trimestre

El càlcul de Q3 es pot fer de la següent manera,

Q3 = ¾ (n + 1) tercer terme

=¾ (11)

P3= 8.25 Termini

El càlcul de la desviació del quartil es pot fer de la següent manera,

• El segon terme és 145 i ara se suma a aquest 0,75 * (150 - 145), que és 3,75 i el resultat és 148,75
• El vuitè mandat és 177 i ara se suma a aquest 0,25 * (188 - 177), que és 2,75 i el resultat és 179,75

Q.D. = Q3 - Q1 / 2

Utilitzant la fórmula de la desviació del quartil, tenim (179.75-148.75) / 2

=31/2

Q.D.=15.50.

Exemple 3

L’acadèmia internacional de Ryan vol analitzar el percentatge de puntuacions dels seus estudiants distribuïts.

Les dades són dels 25 estudiants.

Utilitzeu la fórmula de desviació del quartil per esbrinar la dispersió en% de marques.

Solució:

El nombre d'observacions aquí és 25 i el nostre primer pas seria organitzar les dades en ordre ascendent.

El càlcul de Q1 es pot fer de la següent manera,

Q1 = ¼ (n + 1) tercer terme

=¼ (25+1)

=¼ (26)

P1= 6,5è trimestre

El càlcul de Q3 es pot fer de la següent manera,

Q3 = ¾ (n + 1) tercer terme

=¾ (26)

P3 = 19.50 Termini

El càlcul de la desviació del quartil o del rang semi-intercuartil es pot fer de la següent manera:

• El 6è mandat és 154 i ara se suma a aquest 0,50 * (156 - 154) que és 1 i el resultat és 155,00
• El 19è mandat és 177 i ara se suma a aquest 0,50 * (177 - 177) que és 0 i el resultat és 177

Q.D. = Q3 - Q1 / 2

Utilitzant la fórmula de la desviació del quartil, tenim (177-155) / 2

=22/2

Q.D.= 11.

Exemple # 4

Determinem ara el valor mitjançant una plantilla Excel per a l'exemple pràctic I.

Solució:

Utilitzeu les dades següents per al càlcul de la desviació del quartil.

El càlcul de Q1 es pot fer de la següent manera,

P1=148.75

El càlcul de Q3 es pot fer de la següent manera,

P3= 179.75

El càlcul de la desviació del quartil es pot fer de la següent manera,

Utilitzant la fórmula de la desviació del quartil, tenim (179.75-148.75) / 2

Q.D. serà -

QD = 15.50

Rellevància i usos

Desviació del quartil, que també és coneguda com a gamma semi-intercuartil. De nou, la diferència de la variància entre el 3r i el 1r quartil es denomina rang interquartil. L'interval intercuartil representa fins a quin punt les observacions o els valors del conjunt de dades donat es distribueixen a partir de la mitjana o la seva mitjana. La desviació del quartil o rang semi intercuartil és la majoria que s’utilitza en un cas en què es vol aprendre o dir un estudi sobre la dispersió de les observacions o les mostres dels conjunts de dades donats que es troben al cos principal o mitjà de la sèrie donada. Aquest cas sol passar en una distribució on les dades o les observacions tendeixen a situar-se intensament al cos principal o al centre del conjunt de dades donat o de la sèrie i la distribució o els valors no es troben cap als extrems i, si es troben, no tenen molta importància per al càlcul.