SIN a Excel (fórmula, exemples) | Com s'utilitza la funció Sin en Excel?
La funció SIN Excel és una funció trigonomètrica incorporada a excel que s’utilitza per calcular el valor sinusal d’un nombre determinat o, en termes de trigonometria, el valor sinusal d’un angle determinat, aquí l’angle és un nombre en excel i aquesta funció només adopta un argument que és el número d'entrada proporcionat.
Funció SIN a Excel
La funció SIN a Excel calcula el sinus d'un angle que especifiquem. La funció SIN a Excel es classifica com a funció matemàtica / trigonometria a Excel. SIN a Excel sempre retorna un valor numèric.
En matemàtiques i trigonometria, el SINE és una funció trigonomètrica d’un angle, que en un triangle rectangle és igual a la longitud del costat oposat (el costat rectangle), dividit per la longitud de la hipotenusa, i representat com :
Sin Θ = costat oposat / hipotenusa

Sin Θ = a / h
Fórmula SIN a Excel
A continuació es mostra la fórmula SIN a Excel.

On nombre és un argument passat a la fórmula SIN en radians.
Si passem directament l’angle a SIN en la funció excel, no el reconeixerà com un argument vàlid. Per exemple, si passem 30 ° com a argument a aquest SIN a la funció Excel, no el reconeixerà com a argument vàlid. L’Excel mostrarà un missatge d’error.

Per tant, l’argument que hem d’aprovar ha d’estar inclòs radians.
Per convertir un angle en radian, hi ha dos mètodes
- Utilitzeu la funció Excel RADIANS incorporada. La funció RADIANS converteix els graus en un valor radian.
Per exemple, per convertir 30 ° a radian utilitzarem aquesta funció, pren el grau com a nombre, serà de 30 ° com 30.
=RADIANS (30) donarà al radian 0,52

- En el segon cas, podem utilitzar la fórmula matemàtica per a la conversió d’un grau a radian. La fórmula és
Radian = graus * (π / 180) (π = 3,14)
A Excel també tenen una funció que retorna el valor de Pi, precisa a 15 dígits, i la funció és PI()
Per tant, per a la conversió de graus a radians, utilitzaríem la fórmula
Radian = graus * (PI () / 180)
Com s'utilitza la funció SIN a Excel?
La funció SIN a Excel és molt senzilla i fàcil d'utilitzar. Entenguem alguns exemples sobre el funcionament del SIN a Excel.
Podeu descarregar aquesta plantilla SIN a Excel aquí: plantilla SIN a ExcelSIN a Excel, exemple 1
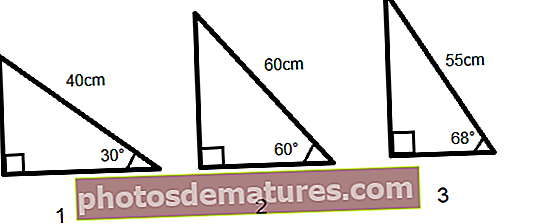
Càlcul del valor sinus mitjançant la funció SIN a Excel i la funció RADIANS a Excel Càlcul del valor sinus mitjançant la funció SIN a Excel i la funció PI La funció Sine a Excel té moltes aplicacions de la vida real; s’utilitza àmpliament en arquitectures per calcular les altures i longituds de les figures geomètriques. També s’utilitza en GPS, òptica, càlcul de trajectòries, per trobar la ruta més curta en funció de la ubicació geogràfica de latitud i longitud, emissió de ràdio, etc. Fins i tot es representa una ona electromagnètica com a gràfic de la funció sinus i cosinus. Suposem que tenim tres triangles rectangles, donats amb els seus angles i longitud d’un costat i que hem de calcular la longitud dels altres dos costats. La suma de tots els angles d’un triangle és igual a 180 °, per tant, podem calcular fàcilment el tercer angle. Sabem, Sin Θ = oposat / hipotenusa Per tant, la longitud del costat oposat serà Sin Θ * hipotenusa A Excel, la longitud del costat oposat (costat perpendicular) es calcularà mitjançant la fórmula SIN = PECAT (RADIANS (C2)) * E2 Aplicant la fórmula SIN donada anteriorment per a tres triangles podem obtenir la longitud de les perpendiculars dels triangles Per al tercer costat (costat adjacent), tenim dos mètodes: utilitzant el teorema de Pitàgores o utilitzant de nou la funció SIN a Excel des d'altres angles. Segons el teorema de Pitàgores, la suma de quadrats de dos costats del triangle rectangle és equivalent al quadrat de la hipotenusa. Hipotenusa2 = oposada2 + adjacent2 Adjacent = (Hipotenusa2 - Contrari2) 1/2 En Excel, l’escriureem com: = PODER ((PODER (Hipotenusa, 2) -PODER (oposat, 2)), 1/2) Aplicant aquesta fórmula, calculem la longitud del costat adjacent = POTÈNCIA ((POTÈNCIA (E2,2) -POTÈNCIA (F2,2)), 1/2) Mitjançant el segon mètode, podem utilitzar el SINE del 3r angle per calcular el valor del costat adjacent Si girem els triangles a 90 ° a l’esquerra, el costat oposat s’intercanvia amb el costat adjacent i el SIN d’angle entre hipotenusa i adjacent ajudarà a calcular el valor del tercer costat. = PECAT (RADIANS (D2)) * E2 Hi ha un edifici alt d’alçada desconeguda i el raig solar en un punt del temps fa un angle en el punt A de 75 °, fent així una ombra de l’edifici de 70 metres de longitud. Hem de trobar l’alçada de la torre L'alçada de la construcció es calcularà mitjançant la funció SIN en excel SIN 75 ° = Alçada de l’edifici / Longitud de l’ombra al punt A Per tant, l'alçada de l'edifici = SIN 75 ° * Longitud de l’ombra al punt A Per tant, l’altura de la construcció serà = PECAT (RADIANS (B3)) * B2 L'altura de l'edifici és de 67,61 metres Tenim un terreny en forma de triangle, per al qual els dos angles es donen com a 30 ° i 70 ° i només coneixem la longitud d’un costat del triangle que és de 40 metres. Hem de trobar la longitud d’altres tres costats i el perímetre del triangle. Per a un triangle, quan es coneix un costat i tots els angles, podem calcular els altres costats mitjançant la regla SINE La regla sinusal de la trigonometria dóna una relació d'angles de sin i costats d'un triangle mitjançant una fórmula SIN a / sin α = b / sin ß = c / sin δ En aquest cas, α = 30 °, ß = 70 ° i δ = 180 ° - (30 ° + 70 °) = 80 ° i un costat del triangle b = 40 metres Per trobar els altres costats del triangle utilitzarem la regla SINE a = Sin α * (b / sin ß) Per tant, a = SIN (RADIANS (30)) * (B5 / SIN (RADIANS (70))) Longitud del costat a = 21,28 metres De la mateixa manera, la tercera cara c serà c = Sin δ * (b / sin ß) Per tant, c = SIN (RADIANS (80)) * (B5 / SIN (RADIANS (70))) Els tres costats del triangle tenen una longitud de 21,28, 40, 41,92 metres. El perímetre del triangle és la suma de tots els costats. Per tant, el perímetre serà = SUMA (B5: B7)











SIN a Excel, exemple 2



SIN a Excel, exemple 3