photosdematures.com

Definició del coeficient de correlació de Pearson

El coeficient de correlació de Pearson, també conegut com a prova estadística de Pearson R, mesura la força entre les diferents variables i les seves relacions. Sempre que es realitza alguna prova estadística entre les dues variables, sempre és una bona idea que la persona que fa anàlisi calculi el valor del coeficient de correlació per saber que tan forta és la relació entre les dues variables.

El coeficient de correlació de Pearson retorna un valor entre -1 i 1. La interpretació del coeficient de correlació és la següent:

• Si el coeficient de correlació és -1, indica una forta relació negativa. Implica una perfecta relació negativa entre les variables.
• Si el coeficient de correlació és 0, no indica cap relació.
• Si el coeficient de correlació és 1, indica una forta relació positiva. Implica una perfecta relació positiva entre les variables.

Un valor absolut més alt del coeficient de correlació indica una relació més forta entre variables. Per tant, un coeficient de correlació de 0,78 indica una correlació positiva més forta en comparació amb un valor de 0,36. De la mateixa manera, un coeficient de correlació de -0,87 indica una correlació negativa més forta en comparació amb un coeficient de correlació de -0,40.

Dit d'una altra manera, si el valor està en l'interval positiu, mostra que la relació entre variables es correlaciona positivament i que els dos valors disminueixen o augmenten junts. D'altra banda, si el valor està en l'interval negatiu, mostra que la relació entre variables es correlaciona negativament i que els dos valors aniran en la direcció oposada.

Fórmula del coeficient de correlació de Pearson

La fórmula del coeficient de correlació de Pearson és la següent,

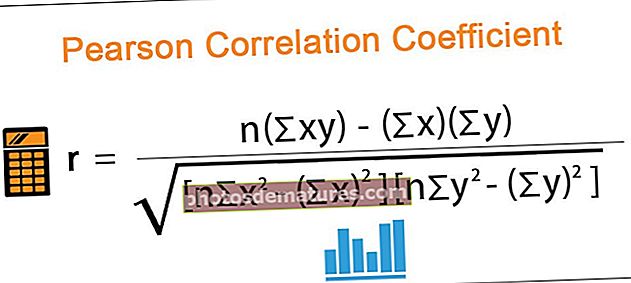
On,

• r = Coeficient de Pearson
• n = nombre dels parells del brou
• ∑xy = suma de productes de les existències aparellades
• ∑x = suma de les x puntuacions
• ∑y = suma de les puntuacions y
• ∑x2 = suma de les x puntuacions al quadrat
• ∑y2 = suma de les puntuacions y al quadrat

Explicació

Pas 1: Esbrineu el nombre de parells de variables, que es denota amb n. Suposem que x consta de 3 variables: 6, 8, 10. Suposem que y consisteix en 3 variables 12, 10, 20 corresponents.

Pas 2: Enumereu les variables en dues columnes.

Pas 3: Esbrineu el producte de xey a la 3a columna.

Pas 4: Esbrineu la suma de valors de totes les variables x i de totes les variables y. Escriviu els resultats a la part inferior de la 1a i la 2a columna. Escriviu la suma de x * y a la 3a columna.

Pas 5: Esbrineu x2 i y2 a les 4a i 5a columnes i la seva suma a la part inferior de les columnes.

Pas 6: Inseriu els valors que es troben a la fórmula anterior i resoleu-los

r = 3 * 352-24 * 42 / √ (3 * 200-242) * (3 * 644-422)

= 0.7559

Exemple de coeficient de correlació Pearson R

Podeu descarregar aquesta plantilla Excel del coeficient de correlació de Pearson aquí - Plantilla Excel del coeficient de correlació de Pearson

Exemple 1

En aquest exemple, amb l'ajut dels detalls següents a la taula de les 6 persones que tenen una edat i pesos diferents que es donen a continuació per al càlcul del valor del Pearson R

Solució:

Per al càlcul del coeficient de correlació de Pearson, primer calcularem els valors següents,

Aquí el nombre total de persones és de 6, de manera que n = 6

Ara el càlcul del Pearson R és el següent,

• r = (n (∑xy) - (∑x) (∑y)) / (√ [n ∑x2- (∑x) 2] [n ∑y2– (∑y) 2)
• r = (6 * (13937) - (202) (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
• r = (6 * (13937) - (202) * (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
• r = (83622- 82618) / (√ [43680 -40804] * [170190- 167281)
• r = 1004 / (√ [2876] * [2909)
• r = 1004 / (√ 8366284)
• r = 1004 / 2892,452938
• r = 0,35

Per tant, el valor del coeficient de correlació de Pearson és 0.35

Exemple 2

Hi ha 2 accions: A i B. Els preus de les accions en dies concrets són els següents:

Esbrineu el coeficient de correlació de Pearson a partir de les dades anteriors.

Solució:

En primer lloc, calcularem els valors següents.

El càlcul del coeficient de Pearson és el següent,

• r = (5*1935-266*37)/((5*14298-(266)^2)*(5*283-(37)^2))^0.5
• = -0.9088

Per tant, el coeficient de correlació de Pearson entre les dues existències és de -0,9088.

Avantatges

• Ajuda a saber fins a quin punt és forta la relació entre les dues variables. No només s’indica la presència o l’absència de la correlació entre les dues variables mitjançant el coeficient de correlació de Pearson, sinó que també determina la mesura exacta en què es correlacionen aquestes variables.
• Mitjançant aquest mètode, es pot determinar la direcció de la correlació, és a dir, si la correlació entre dues variables és negativa o positiva.

Desavantatges

• El coeficient de correlació de Pearson R no és suficient per diferenciar les variables dependents i les variables independents, ja que el coeficient de correlació entre les variables és simètric. Per exemple, si una persona intenta conèixer la correlació entre l’alta tensió i la pressió arterial, es pot trobar l’alt valor de la correlació que demostra que l’alta tensió provoca la pressió arterial. Ara bé, si es canvia la variable, el resultat, en aquest cas, també serà el mateix que demostra que l'estrès és causat per la pressió arterial, que no té sentit. Per tant, l'investigador hauria de ser conscient de les dades que utilitza per dur a terme l'anàlisi.
• Mitjançant aquest mètode no es pot obtenir la informació sobre el pendent de la línia, ja que només indica si existeix o no alguna relació entre les dues variables.
• És probable que el coeficient de correlació de Pearson es pugui malinterpretar sobretot en cas de dades homogènies.
• Si es compara amb els altres mètodes de càlcul, aquest mètode triga molt a arribar als resultats.

Punts importants

• Els valors poden anar des del valor +1 fins al valor -1, on el +1 indica la relació positiva perfecta entre les variables considerades, el -1 indica la relació negativa perfecta entre les variables considerades i un valor 0 indica que no hi ha relació existeix entre les variables considerades.
• És independent de la unitat de mesura de les variables. Per exemple, si la unitat de mesura d'una variable és en anys mentre que la unitat de mesura de la segona variable és en quilograms, fins i tot llavors, el valor d'aquest coeficient no canvia.
• El coeficient de correlació entre les variables és simètric, cosa que significa que el valor del coeficient de correlació entre Y i X o X i Y seguirà sent el mateix.

Conclusió

El coeficient de correlació de Pearson és el tipus de coeficient de correlació que representa la relació entre les dues variables que es mesuren en el mateix interval o en la mateixa escala de relació. Mesura la força de la relació entre les dues variables contínues.

No només indica la presència o l'absència de la correlació entre les dues variables, sinó que també determina la mesura exacta amb què es correlacionen aquestes variables. És independent de la unitat de mesura de les variables on els valors del coeficient de correlació poden anar des del valor +1 fins al valor -1. Tot i això, no n’hi ha prou amb diferenciar entre les variables dependents i les variables independents.