Diferència entre la prova Z i la prova T de la prova d’hipòtesi
Diferències entre la prova Z i la prova T.
Prova Z és la hipòtesi estadística que s’utilitza per determinar si les dues mostres calculades són diferents si la desviació estàndard està disponible i la mostra és gran mentre que Prova T s’utilitza per determinar com difereixen les mitjanes de diferents conjunts de dades entre si en cas que no es conegui la desviació estàndard o la variància.
Les proves Z i les proves t són els dos mètodes estadístics que impliquen anàlisi de dades que té aplicacions en ciències, negocis i moltes altres disciplines. La prova t es pot referir a una prova hipòtesi univariant que es basa en l’estadística t, en la qual es coneix la mitjana, és a dir, la mitjana, i la variància de la població, és a dir, la desviació estàndard s’aproxima de la mostra. D'altra banda, la prova Z, també una prova univariant que es basa en una distribució normal estàndard.

Usos
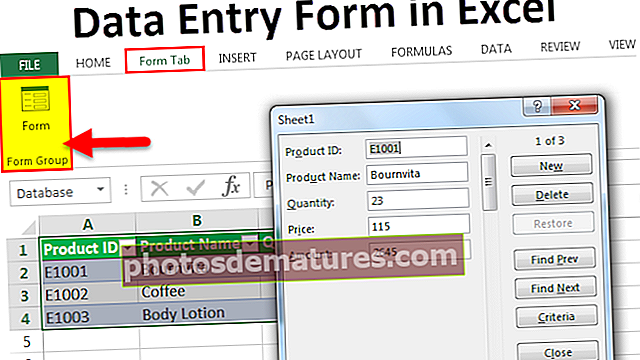
# 1 - Prova Z
La fórmula de la prova Z, com s’ha esmentat anteriorment, són els càlculs estadístics que es poden utilitzar per comparar les mitjanes poblacionals amb les d’una mostra. La prova z us indicarà fins a quin punt, en termes de desviacions estàndard, es troba un punt de dades respecte a la mitjana d’un conjunt de dades. Una prova z farà una comparació d’una mostra amb una població definida que s’utilitza normalment per tractar problemes relacionats amb mostres grans (és a dir, n> 30). Sobretot, són molt útils quan es coneix la desviació estàndard.
# 2 - Prova T
Les proves T també són càlculs que es poden utilitzar per provar una hipòtesi, però són molt útils quan hem de determinar si hi ha una comparació estadísticament significativa entre els 2 grups de mostra independents. Dit d’una altra manera, una prova t pregunta si és probable que la comparació entre les mitjanes de 2 grups no s’hagi produït a causa de l’atzar. Normalment, les proves t són més apropiades quan es tracta de problemes amb una mida de mostra limitada (és a dir, n <30).
Z-Test vs T-Test Infographics
Aquí us proporcionem les 5 diferències principals entre la prova z i la prova t que heu de conèixer.

Diferències clau
- Una de les condicions més importants per dur a terme una prova t és que es desconeix la desviació estàndard de la població o la variància. Per contra, s’ha de suposar que la fórmula de variància poblacional, tal com s’ha dit anteriorment, és coneguda o coneguda en cas de fer una prova z.
- La prova t esmentada anteriorment es basa en la distribució t de Student. Per contra, la prova z depèn de la suposició que la distribució de les mostres serà normal. Tant la distribució normal com la distribució t de l’alumne apareixen igual, ja que totes dues tenen forma de campana i són simètriques. No obstant això, es diferencien en un dels casos que en la distribució en at, hi ha menys espai al centre i més a la cua.
- La prova Z s’utilitza tal com s’indica a la taula anterior quan la mida de la mostra és gran, que és n> 30, i la prova t és adequada quan la mida de la mostra no és gran, és a dir, n <30.
Taula comparativa Z-Test vs T-Test
| Bases | Prova Z | Prova T | ||
| Definició bàsica | La prova Z és una mena de prova d’hipòtesis que determina si les mitjanes dels dos conjunts de dades són diferents entre si quan es dóna una desviació estàndard o una variància. | La prova t es pot referir a una mena de prova paramètrica que s'aplica a una identitat, en què es diferencien les mitjanes de 2 conjunts de dades entre si quan no es dóna la desviació estàndard o la variància. | ||
| Variació de la població | Aquí es coneix la variància poblacional o desviació estàndard. | Aquí es desconeix la variància poblacional o la desviació estàndard. | ||
| Grandària de la mostra | La mida de la mostra és gran | Aquí la mida de la mostra és petita. | ||
| Supòsits clau |
|
| ||
| Basat en (un tipus de distribució) | Basat en la distribució normal. | Basat en la distribució Student-t. |
Conclusió
En gran mesura, ambdues proves són gairebé similars, però la comparació només arriba a les seves condicions per a la seva aplicació, el que significa que la prova t és més adequada i aplicable quan la mida de la mostra no és superior a trenta unitats. Tanmateix, si és superior a trenta unitats, s'hauria d'utilitzar una prova z. De la mateixa manera, també hi ha altres condicions, que deixaran clar que quina prova es realitzarà en una situació.
Bé, també hi ha diferents proves, com ara la prova f, de dues cues vs de cua simple, etc., els estadístics han de tenir precaució mentre els apliquen després d’analitzar la situació i després decidir quina utilitzar. A continuació es mostra un gràfic de mostra del que hem comentat anteriorment.