Matriu de covariància a Excel | Guia pas a pas (amb exemples)
Matriu de covariància en excel
La matriu de covariància és una matriu quadrada per mostrar la covariància entre les columnes i la variància en columnes. Excel presenta una eina d’anàlisi de dades incorporada per determinar la covariància entre els diferents conjunts de dades. El present article explicarà el càlcul de la matriu de covariància a Excel tractant els temes següents, inclosos:
Explicació
La covariància és una de les mesures que s’utilitzen per entendre com s’associa una variable a una altra variable. La següent fórmula s’utilitza per determinar la covariància.
COV (X, Y) = ∑ (x - x) (y - y) / n
La matriu de covariància és una matriu quadrada per entendre les relacions presentades entre les diferents variables d’un conjunt de dades. És fàcil i útil mostrar la covariància entre dues o més variables.
La covariància tindrà tant valors positius com negatius. Un valor positiu indica que dues variables disminuiran o augmentaran en la mateixa direcció. Un valor negatiu indica que si una variable disminueix, augmenta una altra variable i existeix una relació inversa entre elles. La matriu de covariància es representa en el format següent. La matriu de covariància tridimensional es mostra com

Per crear la matriu de covariància quadrada 3 × 3, hem de tenir dades tridimensionals. Els valors diagonals de la matriu representen les variàncies de les variables X, Y i Z (és a dir, COV (X, X), COV (Y, Y) i COV (Z, Z)). La matriu de covariància és simètrica respecte a la diagonal. Això indica que COV (X, Y) = COV (Y, X), COV (X, Z) = COV (Z, X) i COV (Y, Z) = COV (Z, Y). Un punt que cal recordar sobre aquesta matriu és el resultat de la matriu de covariança NXN per a dades de dimensió n.

Com s'utilitza una matriu de covariància a Excel?
La matriu de covariància s'utilitza en diverses aplicacions, incloses
- Analitzant com dos vectors es diferencien entre si
- S'utilitza en l'aprenentatge automàtic per determinar els patrons de dependència entre els dos vectors
- La matriu de covariància s'utilitza per explicar la relació entre les diferents dimensions de variables aleatòries
- S'utilitza en models estocàstics en enginyeria financera per correlacionar les variables aleatòries
- Component de principi és una altra aplicació de la matriu de covariància a variables originals a variables independents lineals
- En l’anàlisi de dades, la matriu de covariància té un paper vital.
- La matriu de covariància s'utilitza en la teoria moderna de carteres per a l'estimació de riscos.
- Les mesures de la matriu de covariància s’utilitzen per anticipar els rendiments dels actius financers
Exemples de matriu de covariància a Excel
A continuació es detallen alguns exemples per utilitzar la matriu de covariància en excel.
Podeu descarregar aquesta plantilla Excel de matriu de covariança aquí: plantilla Excel de matriu de covariançaExemple 1
Realització d’anàlisis de covariància sobre les notes obtingudes pels estudiants en diferents matèries.
Pas 1: Les dades següents, incloses les notes dels estudiants de matemàtiques, anglès i ciències, es consideren tal com es mostra a la figura.

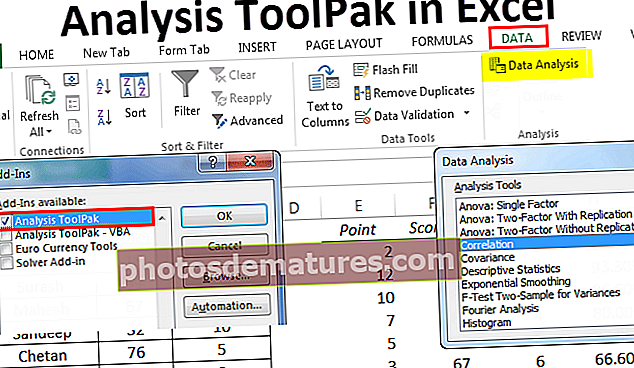
Pas 2: Aneu a la pestanya "Dades" de la cinta i cerqueu el ToolPak "Anàlisi de dades" a la cantonada dreta.
Si ToolPak "Anàlisi de dades" no està disponible, seguiu aquests passos
Pas A: Aneu a la pestanya "Fitxer" i seleccioneu les "opcions".

S'obrirà la següent pantalla.

Pas B: Aneu a Complements. A l'opció Gestiona l'opció, assegureu-vos que estigueu seleccionat "Complements d'Excel" i seleccioneu el botó "Vés" tal com es mostra a la figura.

Pas C: Seleccioneu "Analysis-Tool Pak" i "Analysis-ToolPak VBA" com es mostra a la captura de pantalla.

Després de completar aquests passos, l'eina pak "Anàlisi de dades" s'afegeix a la pestanya "Dades".

Pas 3: Feu clic a Anàlisi de dades. S'obrirà el quadre de diàleg "Anàlisi de dades". Seleccioneu la "Covariança" desplaçant-vos cap amunt i feu clic a "D'acord".

Es mostra el quadre de diàleg "Covariança".

Pas 5: Seleccioneu l'interval d'entrada, inclosos els noms del tema, marqueu les "etiquetes de primera fila" i doneu el "rang de sortida" al full de treball existent. I feu clic a "D'acord".

Pas 6: Obtindrem la sortida de la següent manera:

La part superior de la diagonal està buida ja que la matriu de covariança excel és simètrica cap a la diagonal.
Exemple 2
Càlcul de la matriu de covariança per determinar les variacions entre els rendiments de diferents accions de cartera.
Pas 1: Per a aquest exemple, es consideren les dades següents, incloses les declaracions de valors.

Pas 2: Obre el quadre de diàleg "Anàlisi de dades" i seleccioneu "Covariança" desplaçant-vos cap amunt i feu clic a "D'acord".

Es mostra el quadre de diàleg "Covariança".

Pas 3: Seleccioneu l'interval d'entrada, incloses les capçaleres, marqueu les "etiquetes de primera fila" i doneu el "rang de sortida" al full de treball existent. I feu clic a "D'acord".

Pas 4: Obtindrem la sortida de la següent manera:

La part superior de la diagonal està buida ja que la matriu de covariança és simètrica cap a la diagonal.
Exemple 3
Càlcul de la matriu de covariància per als preus de les accions de les empreses corporatives
Pas 1: Per a aquest exemple, es consideren les dades següents, inclosos els preus de les accions de diferents empreses.

Pas 2: Obre el quadre de diàleg "Anàlisi de dades", seleccioneu la "Covariança" desplaçant-vos cap amunt i feu clic a "D'acord".

Es mostra el quadre de diàleg "Covariança".

Pas 3: Seleccioneu l'interval d'entrada incloses les capçaleres, marqueu les "etiquetes de primera fila" i doneu el "rang de sortida" al full de treball existent i feu clic a "D'acord".

Pas 4: Obtindrem la sortida de la següent manera -

Coses que cal recordar
- L'eina de covariància presentada per Excel té algunes limitacions, inclosa la determinació de la fórmula de les variàncies de la població només, la creació de matriu amb valors diagonals inferiors i la consideració de les fórmules només per a la variància.
- Quan es canvien els valors de retorn, no s’actualitzen automàticament els valors de la matriu.
- La meitat superior de la matriu es mostra buida, ja que és simètrica i els valors de la imatge mirall es mostren a la diagonal inferior.